题目内容
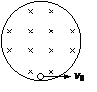
如图12所示，在竖直平面内有一圆形绝缘轨道，半径R=1m，处于垂直于轨道平面向里的匀强磁场中，一质量为
，带电量为
的小球，可在内壁滑动。现在最低点处给小球一个水平初速度v0，使小球在竖直平面内逆时针做圆周运动，图13甲是小球在竖直平面内的速率v随时间变化的情况，图13乙是小球所受轨道的弹力F随时间变化的情况，已知小球能
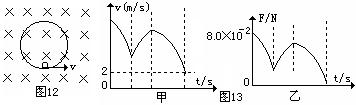
有两次到达圆形轨道的最高点。结合图象和数据（g=10 m/s2），求：
（1）磁感应强度的大小；
（2）小球从开始运动至图甲中速度为2m/s的过程中，摩擦力对小球做的功。
（1）B=0.1T（2）
解析:
（1）由甲图可知，小球第二次过最高点时，速度大小为2m/s，由乙图可知此时轨道与球间的弹力为0，所以有：
，代入数据可得：B=0.1T
（2）从乙图可知小球第一次过最低点时，轨道与球间的弹力为：F=8.0×10-2N，由牛顿第二定律可得：
，解得：v0=7m/s,由于在上过程中洛仑兹力不做功，根据动能定理可得：
，代入数据可得：
练习册系列答案
相关题目
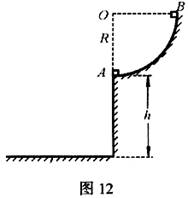如图12所示，在距水平地面高为h处有一半径为R的1/4圆弧轨道，圆弧轨道位于竖直平面内，轨道光滑且末端水平，在轨道的末端静置一质量为m的小滑块A。现使另一质量为m的小滑块B从轨道的最高点由静止释放，并在轨道的最低点与滑块A发生碰撞，碰后粘合为一个小滑块C。已知重力加速度为g。求：
