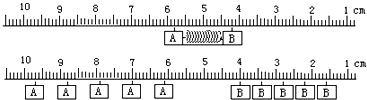
题目内容
(12分)如图12所示，一个竖直放置的圆锥筒可绕其中心轴OO′转动，筒内壁粗糙，筒口半径和筒高分别为R和H，筒内壁A点的高度为筒高的一半．内壁上有一质量为m的小物块．求：
(1)当筒不转动时，物块静止在筒壁A点受到的摩擦力和支持力的大小；
(2)当物块在A点随筒做匀速转动，且其所受到的摩擦力为零时，筒转动的角速度．
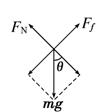
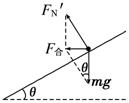
解析：(1)物块静止时，对物块进行受力分析如图所示，设筒壁与水平面的夹角为θ.由平衡条件有
Ff＝mgsinθ FN＝mgcosθ
由图中几何关系有 cosθ＝
， sinθ＝
故有Ff＝
， FN＝
(2)分析此时物块受力如图所示，由牛顿第二定律有
mgtanθ＝mrω2. 其中tanθ＝
，r＝
， 可得ω＝ 
.
练习册系列答案
科学实验活动册系列答案
相关题目
2008年9月25日21时10分，神舟七号飞船成功发射，共飞行2天20小时27分钟，绕地球飞行45圈后，于9月28日17时37分安全着陆．航天员翟志刚着“飞天”舱外航天服，在刘伯明的配合下，成功完成了空间出舱活动，进行了太空行走．出舱活动结束后，释放了伴飞卫星，并围绕轨道舱进行伴飞实验．神舟七号是由长征-2F运载火箭将其送入近地点为A，远地点为B的椭圆轨道上，实施变轨后，进入预定圆轨道，其简化的模拟轨道如图12所示．假设近地点A距地面高度为h，飞船在预定圆轨道上飞行n圈所用的时间为t，地球表面的重力加速度为g，地球半径R，试求：
