Question

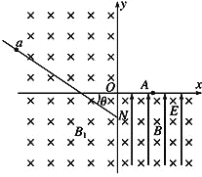
【题目】如图所示，竖直平面内有一直角坐标系 xOy，x轴沿水平方向。第二、三象限有垂直于坐标平面向里的匀强磁场，与 x轴成θ＝37°角的绝缘细杆固定在二、三象限；第四象限同时存在着竖直向上的匀强电场和垂直于坐标平面向里、磁感应强度大小为 B的匀强磁场，一质量为 m、电荷量为q的带电小球 a穿在细杆上沿细杆匀速下滑，在 N点脱离细杆恰能沿圆周轨道运动到 x 轴上的 A 点，且速度方向垂直于 x轴。已知 A点到坐标原点 O的距离为l，小球 a与绝缘细杆的动摩擦因数μ＝0.5；，重力加速度为 g，空气阻力忽略不计。求：

(1)第二、三象限里的磁场的磁感应强度大小 B1与第四象限磁感应强度 B 之比，=？

(2)当带电小球 a 刚离开 A 点竖直向上运动时，从 y 轴正半轴距原点 O为 4l的 P 点（图中未画出）以某一初速度水平向右平抛一个不带电的绝缘小球 b，a、b两球刚好在第一象限某点相碰，则 b球的初速度为多大？

Answer 1

【答案】(1)；(2)

【解析】

(1)由带电小球a在第四象限内做圆周运动，知小球a所受电场力与其重力平衡且小球a所受电场力竖直向上，即

mg=qE

故小球a带正电，解得

带电小球a从N点运动到A点的过程中，洛伦兹力提供小球做圆周运动的向心力，设运动半径为R，有

由几何关系有

解得R=2l，有

带电小球a在杆上匀速下滑时，由平衡条件有

解得

所以

(2)带电小球a在第四象限内做匀速圆周运动的从A点竖直上抛，与b相遇,竖直方向

解得

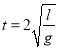
水平方向