题目内容
20.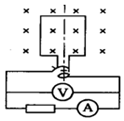 如图所示,线圈的面积是0.05m2,共100匝,线圈电阻为r=1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B=$\frac{\sqrt{2}}{π}$T,当线圈以300r/min的转速匀速旋转时,求:
如图所示,线圈的面积是0.05m2,共100匝,线圈电阻为r=1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B=$\frac{\sqrt{2}}{π}$T,当线圈以300r/min的转速匀速旋转时,求:(1)若从中性面开始计时,写出线圈感应电动势的瞬时表达式.
(2)电路中电压表和电流表的示数各是多少?
(3)由图示位置转过60°角的过程通过电阻R的电荷量为多少?
分析 (1)从线圈处于中性面开始计时,线圈中感应电动势的瞬时值表达式e=Emsinωt,由Em=NBSω求出Em;
(2)交流电压表和电流表测量的是有效值,根据欧姆定律和有效值与最大值的关系求解;
(3)由电流的平均值可得转过60°的过程中通过电阻R的电荷量.
解答 解:(1)若从线圈处于中性面开始计时,线圈中感应电动势的瞬时值表达式为:e=Emsinωt.
其中ω=300r/min=$\frac{300×2π}{60}$=10πrad/s,
Em=NBSω=100×$\frac{\sqrt{2}}{π}$×0.05×10π=50V,
故线圈中感应电动势的瞬时值表达式为:e=50sin10πt.
(2)电动势的有效值为:E=$\frac{{E}_{m}}{\sqrt{2}}$=$\frac{50}{\sqrt{2}}$=25$\sqrt{2}$V
电流表的示数为:I=$\frac{E}{R+r}$=$\frac{25\sqrt{2}}{9+1}$=2.5$\sqrt{2}$A
电压表的示数为:U=IR=2.5$\sqrt{2}$×9=22.5$\sqrt{2}$V
(3)由图示位置转过60°角的过程通过电阻R的电荷量为:
q=N$\frac{△φ}{R+r}$=N$\frac{BScos6{0}^{0}}{R+r}$=100×$\frac{\frac{\sqrt{2}}{π}×0.05}{10}$=$\frac{\sqrt{2}}{2π}$C.
答:(1)从中性面开始计时,线圈感应电动势的瞬时表达式为e=50sin10πt.
(2)电路中电压表22.5$\sqrt{2}$V,电流表的示数为2.5$\sqrt{2}$A;
(3)由图示位置转过60°角的过程通过电阻R的电荷量为$\frac{\sqrt{2}}{2π}$C
点评 本题涉及交流电压与交流电流的瞬时值、最大值、有效值和平均值;瞬时值要注意确定相位,对于电表读数、求产生的热量均由交变电的有效值来确定,而涉及到耐压值时,则由最大值来确定,而通过某一电量时,则用平均值来求.

 阅读快车系列答案
阅读快车系列答案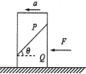 如图所示,质量均为m的两个木块P、Q叠放在水平地面上,P、Q接触面的倾角为θ,现在Q上加一水平推力F,使P、Q保持相对静止一起向左做加速直线运动,下列说法正确的是( )
如图所示,质量均为m的两个木块P、Q叠放在水平地面上,P、Q接触面的倾角为θ,现在Q上加一水平推力F,使P、Q保持相对静止一起向左做加速直线运动,下列说法正确的是( )| A. | 物体Q对地面的压力为mg | |
| B. | 若Q与地面间的动摩擦因数为μ,则μ=$\frac{F}{2mg}$ | |
| C. | 若P、Q之间光滑,则加速度a=gtanθ | |
| D. | 地面与Q间的滑动摩擦力随推力F的增大而增大 |
| A. | pA=6kg?m/s、pB=6kg?m/s | B. | pA=3kg?m/s、pB=9kg?m/s | ||
| C. | pA=2kg?m/s、pB=14kg?m/s | D. | pA=-5kg?m/s、pB=17kg?m/s |
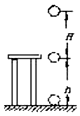 如图从离地面高为h的桌面上以速度v竖直向上抛出质量为m的物体,它上升H后又返回下落,最后落在地面上,则下列说法中正确的是(不计空气阻力,以地面为参考面)( )
如图从离地面高为h的桌面上以速度v竖直向上抛出质量为m的物体,它上升H后又返回下落,最后落在地面上,则下列说法中正确的是(不计空气阻力,以地面为参考面)( )| A. | 物体在最高点时机械能为mg(H+h) | |
| B. | 物体落地时的机械能为mg(H+h)+$\frac{1}{2}$mv2 | |
| C. | 物体落地时的机械能为mgh+$\frac{1}{2}$mv2 | |
| D. | 物体在落回过程中,经过桌面时的机械能为mgH |
 海洋中蕴藏着巨大的能量,利用海洋的波浪可以发电,在我国南海上有一浮筒式波浪发电灯塔,其原理示意图如图甲所示,浮桶内的磁体通过支柱固定在暗礁上,浮桶内置线圈随波浪相对磁体沿竖直方向运动,且始终处于磁场中,该线圈与阻值R=15Ω的灯泡相连.浮桶下部由内、外两密封圆筒构成,(图乙中斜线阴影部分),如图乙所示,其内为产生磁场的磁体,与浮桶内侧面的缝隙忽略不计;匝数N=200的线圈所在处辐向磁场的磁感应强度B=0.2T,线圈直径D=0.4m,电阻r=1Ω.取重力加速度g=10m/s2,π2≈10,若浮筒随波浪上下运动的速度可表示为v=0.4πsin(πt)m/s,则下列说法正确的是( )
海洋中蕴藏着巨大的能量,利用海洋的波浪可以发电,在我国南海上有一浮筒式波浪发电灯塔,其原理示意图如图甲所示,浮桶内的磁体通过支柱固定在暗礁上,浮桶内置线圈随波浪相对磁体沿竖直方向运动,且始终处于磁场中,该线圈与阻值R=15Ω的灯泡相连.浮桶下部由内、外两密封圆筒构成,(图乙中斜线阴影部分),如图乙所示,其内为产生磁场的磁体,与浮桶内侧面的缝隙忽略不计;匝数N=200的线圈所在处辐向磁场的磁感应强度B=0.2T,线圈直径D=0.4m,电阻r=1Ω.取重力加速度g=10m/s2,π2≈10,若浮筒随波浪上下运动的速度可表示为v=0.4πsin(πt)m/s,则下列说法正确的是( )| A. | 灯泡的电功率为120W | |
| B. | 波浪发电产生电动势e的瞬间表达式为c=16sin(πt)V | |
| C. | 灯泡两端电压的有效值为$\frac{15\sqrt{2}}{2}$V | |
| D. | 灯泡中电流i的瞬时表达式为i=4sin(πt)A |
| A. | 竖直分速度与水平分速度大小相等 | B. | 瞬时速度大小vt=$\sqrt{5}{v_0}$ | ||
| C. | 运动的时间t=$\frac{{2{v_0}}}{g}$ | D. | 位移大小等于s=$\frac{{2\sqrt{2}{v_0}^2}}{g}$ |
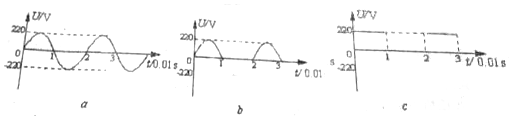
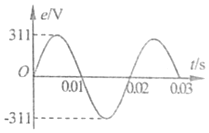 在匀强磁场中,一矩形金属线圈绕与磁场方向垂直的轴匀速转动,产生的电动势随时间变化的图象如图所示.则( )
在匀强磁场中,一矩形金属线圈绕与磁场方向垂直的轴匀速转动,产生的电动势随时间变化的图象如图所示.则( )| A. | t=0时刻线圈平面与中性面重合 | B. | t=0.01s时穿过线圈的磁通量最小 | ||
| C. | 电动势的频率为0.02Hz | D. | 电动势的有效值为31IV |