题目内容
（18分）如图所示，在x轴下方的区域内存在+y方向的匀强电场，电场强度为E。在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场，磁场的方向垂直于xoy平面向外，磁感应强度为B。-y轴上的A点与O点的距离为d，一个质量为m、电荷量为q的带正电粒子从A点由静止释放，经电场加速后从O点射入磁场，不计粒子的重力。 
（1）求粒子在磁场中运动的轨道半径r；
（2）要使粒子进人磁场之后不再经过x轴，求电场强度的取值范围；
（3）改变电场强度，使得粒子经过x轴时与x轴成θ=300的夹角，求此时粒子在磁场中的运动时间t及经过x轴的位置坐标值x0。
（1）
（2）
（3）
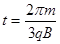
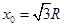
解析试题分析：（1）粒子在电场中加速，由动能定理得： 11
① -------（2分）
粒子进入磁场后做圆周运动，有：
② ----（2分）
解得粒子在磁场中运动的半径： ③ -------（2分）
（2）设场强为E0时，粒子离开磁场后恰好不再经过x轴，则离开磁
场时的速度方向与x轴平行，运动情况如图（甲），
易得：
④ --------（2分）
由③、④式解得：
⑤ -----------（2分）
因此，场强的范围：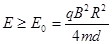
⑥ -------（1分）
（3）粒子运动情况如图（乙），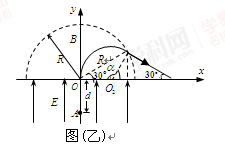
由几何关系可得：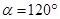
⑦ -------（2分）
粒子在磁场中的运动周期为：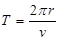
⑧--------（1分）
粒子在磁场中的运动周期为：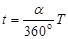
⑨--------（1分）
联立②⑥⑦⑧可得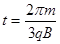： ⑩--------（1分）
由图可得粒子经过x轴时的位置横坐标值为：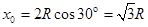 
--------（2分）
阅读快车系列答案
＝37°，则匀强电场的场强大小为_________v/m，电场强度的方向为______(COS37°＝0.8).
＝1×108 C/kg、初速度为v0＝2×105 m/s的带正电粒子。忽略粒子重力以及它们之间的相互作用． 
如图所示，匀强磁场的方向垂直于光滑的金属导轨平面向里，极板间距为d的平行板电容器与总阻值为2R0的滑动变阻器通过平行导轨连接，电阻为R0的导体棒MN可在外力的作用下沿导轨从左向右做匀速直线运动。当滑动变阻器的滑动触头位于a、b的中间位置且导体棒MN的速度为v0时，位于电容器中P点的带电油滴恰好处于静止状态。若不计摩擦和平行导轨及导线的电阻，各接触处接触良好，重力加速度为g，则下列判断正确的是
| A．油滴带正电荷 |
| B．若将上极板竖直向上移动距离d，油滴将向上加速运动，加速度a = g/2 |
| C．若将导体棒的速度变为2v0，油滴将向上加速运动，加速度a = g |
| D．若保持导体棒的速度为v0不变，而将滑动触头置于a端，同时将电容器上极板向上移动距离d/3，油滴仍将静止 |
的电子从
点沿与电场垂直的方向进入匀强电场，初速度为
，当它通过电场中
点时，速度与场强方向成
角，不计电子的重力，求：
两点间的电势差多大。
