题目内容
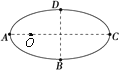
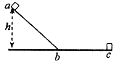
【题目】图是某游乐场的一种过山车的简化图，过山车由倾角为
的斜面和半径为R的光滑圆环组成。假设小球从A处由静止释放，沿着动摩擦因数为μ的斜面运动到B点（B为斜面与圆环的切点），而后沿光滑圆环内侧运动，若小球刚好能通过圆环的最高点C。（重力加速度为g）求：
(1)小球经过圆环最低点D时轨道对小球支持力的大小；
(2)A、B之间的距离。
【答案】(1)6mg；(2)
【解析】
(1)小球刚好能通过圆环最高点，由牛顿第二定律得
小球在圆环最低点时由牛顿第二定律得
小球由D点运动到C点的过程中机械能守恒
由以上各式得
(2)设A、B间的距离为L，小球沿斜面由A运动到B的过程，根据动能定理得
小球由B点运动到C点的过程由机械能守恒得
又由几何关系可得
由以上各式解得
练习册系列答案
华东师大版一课一练系列答案
相关题目
