题目内容
在游乐场中,有一大型游戏机叫“跳楼机”,参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面40米高处,然后自由释放.为研究方便,可以认为座椅沿轨道自由下落1.2s后,开始受到压缩空气提供的恒定阻力而立即做匀减速运动,且下落到离地面4.0米高处时速度恰好减小到零,然后再让座椅缓慢下落,将游客送回地面,取g=10m/s2,求:
(1)座椅自由下落的高度是多少?座椅自由下落结束时刻的速度是多少?
(2)在匀减速阶段,座椅对游客的作用力大小是游客体重的多少倍?
解:(1)座椅自由下落阶段高度 h1= gt12=7.2m
gt12=7.2m
座椅自由下落结束时速度 v1=gt1=12 m/s
(2)匀减速阶段h2=40-4-7.2=28.8 m
根据速度位移关系公式,有:a2=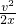 ,
,
解得a2=2.5m/s2(方向竖直向上)
依F合=ma
F-mg=ma2
解得F=3.5mg
答:(1)座椅自由下落的高度是7.2m,座椅自由下落结束时刻的速度是12 m/s;
(2)在匀减速阶段,座椅对游客的作用力大小是游客体重的3.5倍.
分析:(1)根据位移时间关系公式和速度世间关系公式列式求解即可;
(2)先根据速度位移关系公式求解加速度,然后受力分析并根据牛顿第二定律列式求解.
点评:本题关键根据运动学公式确定加速度,然后根据牛顿第二定律确定受力情况,基础题.
 gt12=7.2m
gt12=7.2m 座椅自由下落结束时速度 v1=gt1=12 m/s
(2)匀减速阶段h2=40-4-7.2=28.8 m
根据速度位移关系公式,有:a2=
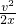 ,
,解得a2=2.5m/s2(方向竖直向上)
依F合=ma
F-mg=ma2
解得F=3.5mg
答:(1)座椅自由下落的高度是7.2m,座椅自由下落结束时刻的速度是12 m/s;
(2)在匀减速阶段,座椅对游客的作用力大小是游客体重的3.5倍.
分析:(1)根据位移时间关系公式和速度世间关系公式列式求解即可;
(2)先根据速度位移关系公式求解加速度,然后受力分析并根据牛顿第二定律列式求解.
点评:本题关键根据运动学公式确定加速度,然后根据牛顿第二定律确定受力情况,基础题.

练习册系列答案
相关题目