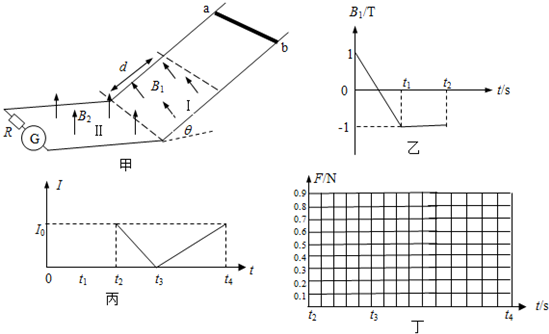
题目内容
18.如图所示,遥控电动赛车(可视为质点)从A点由静止出发,经过时间t后关闭电动机,赛车继续前进至B点后进入固定在竖直平面内的圆形光滑轨道,通过轨道最高点P后又进入水平轨道CD上.已知赛车在水平轨道AB部分和CD部分运动时受到阻力恒为车重的0.5倍,赛车的质量m=0.4kg,通电后赛车的电动机以额定功率P=2W工作,轨道AB的长度L=2m,圆形轨道的半径R=0.5m,空气阻力可忽略,取重力加速度g=10m/s2.某次比赛,要求赛车在运动过程中刚好通过轨道的最高点P.在此条件下,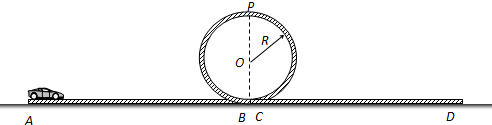
求:(1)小车在CD轨道上运动的路程.
(2)赛车运动到圆形光滑轨道最底部时对轨道的压力.
(3)赛车电动机工作的时间.
分析 (1)对P点到停下这段过程运用动能定理,求出在CD轨道上运动的路程;
(2)从C点运动到最高点D的过程中,根据机械能守恒求得最高点D速度,根据牛顿第二定律求得对轨道压力;
(3)对A到P段运用动能定理,抓住功率不变,求出电动机工作的时间.
解答 解:(1)要使小车恰好通过最高点,根据mg=$m\frac{{v}_{p}^{2}}{R}$
得:${v}_{p}=\sqrt{gR}$=$\sqrt{10×0.5}m/s=\sqrt{5}m/s$
根据动能定理得:$mg•2R-kmg•{x}_{CD}=0-\frac{1}{2}m{v}_{p}^{2}$
代入数据解得:xCD=2.5m.
(2)从C点运动到最高点D的过程中,机械能守恒得$\frac{1}{2}m{v}_{c}^{2}=\frac{1}{2}m{v}_{D}^{2}+mgR(1+cosα)$
设赛车经过最高点D处时对轨道压力FN
${F}_{N}+mg=m\frac{{v}_{D}^{2}}{R}$
联立解得FN=1.6N
(3)对A到P段运用动能定理得:Pt-kmgL-mg•2R=$\frac{1}{2}m{v}_{p}^{2}$
代入数据解得:t=4.5s.
答:(1)车在CD轨道上运动的最短路程为2.5m;
(2)赛车运动到圆形光滑轨道最底部时对轨道的压力为1.6N.
(3)赛车电动机工作的时间为4.5s
点评 本题考查了动能定理和牛顿第二定律的综合运用,运用动能定理解题关键选择好研究的过程,分析过程中有哪些力做功,然后根据动能定理列式求解.

练习册系列答案
相关题目
9.在以下各种说法中,正确的是 ( )
| A. | 做简谐运动的质点,其振动能量与振幅无关 | |
| B. | 两个相邻的、在振动过程中对平衡位置的位移总是相等的质点之间的距离为一个波长 | |
| C. | 两列频率相同的声波在空气中发生干涉时,振动加强质点的位移一定大于振动减弱质点的位移 | |
| D. | 若波源向观察者靠近,则波源发出的波的频率变大 | |
| E. | 泊松亮斑说明光具有衍射现象,小孔成像说明光不具有衍射现象 | |
| F. | 电磁波的传播不需要介质,声波的传播一定需要介质 | |
| G. | 非均匀变化的电场能产生变化的磁场,反之,变化的磁场一定产生非均匀变化的电场 | |
| H. | 真空中的光速在不同的惯性参考系中都是相同的,与光源的运动和观察者的运动无关. |
6. 为了测量某化工厂污水排放量,技术人员在该厂的排污管末端安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c,左右两端开口,在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个内侧固定有金属板作为电极,污水充满管口以一定的速度从左向右流经该装置时,电压表将显示两个电极间的电压U.若用Q表示污水流量(单位时间内排出的污水体积),下列说法中正确的是( )
为了测量某化工厂污水排放量,技术人员在该厂的排污管末端安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c,左右两端开口,在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个内侧固定有金属板作为电极,污水充满管口以一定的速度从左向右流经该装置时,电压表将显示两个电极间的电压U.若用Q表示污水流量(单位时间内排出的污水体积),下列说法中正确的是( )
 为了测量某化工厂污水排放量,技术人员在该厂的排污管末端安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c,左右两端开口,在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个内侧固定有金属板作为电极,污水充满管口以一定的速度从左向右流经该装置时,电压表将显示两个电极间的电压U.若用Q表示污水流量(单位时间内排出的污水体积),下列说法中正确的是( )
为了测量某化工厂污水排放量,技术人员在该厂的排污管末端安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c,左右两端开口,在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个内侧固定有金属板作为电极,污水充满管口以一定的速度从左向右流经该装置时,电压表将显示两个电极间的电压U.若用Q表示污水流量(单位时间内排出的污水体积),下列说法中正确的是( )| A. | 若污水中正离子较多,则前表面比后表面电势高 | |
| B. | 前表面的电势一定低于后表面的电势,与哪种离子多无关 | |
| C. | 污水中离子浓度越高,电压表的示数将越大 | |
| D. | 污水流量Q与U成正比,与a、b无关 |
13. 如图所示,一理想变压器原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,将原线圈接在u=200$\sqrt{2}$sin100πt(V)的交流电压上,副线圈上电阻R和理想交流电压表并联接入电路,现在A、B两点间接入不同的电子元件,则下列说法正确的是( )
如图所示,一理想变压器原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,将原线圈接在u=200$\sqrt{2}$sin100πt(V)的交流电压上,副线圈上电阻R和理想交流电压表并联接入电路,现在A、B两点间接入不同的电子元件,则下列说法正确的是( )
 如图所示,一理想变压器原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,将原线圈接在u=200$\sqrt{2}$sin100πt(V)的交流电压上,副线圈上电阻R和理想交流电压表并联接入电路,现在A、B两点间接入不同的电子元件,则下列说法正确的是( )
如图所示,一理想变压器原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,将原线圈接在u=200$\sqrt{2}$sin100πt(V)的交流电压上,副线圈上电阻R和理想交流电压表并联接入电路,现在A、B两点间接入不同的电子元件,则下列说法正确的是( )| A. | 在A、B两点间串联一只电阻R,穿过铁芯的磁通量的最大变化率为0.2Wb/s | |
| B. | 在A、B两点间接入理想二极管,电压表读数为40V | |
| C. | 在A、B两点间接入一只电容器,只提高交流电频率,电压表读数增大 | |
| D. | 在A、B两点间接入一只电感线圈,只提高交流电频率,电阻R消耗电功率减小 |
8.下列说法中正确的是( )
| A. | 物体在恒力作用下不可能作曲线运动 | |
| B. | 物体在变力作用下一定作曲线运动 | |
| C. | 曲线运动一定是变速运动 | |
| D. | 曲线运动可能是匀加速运动 |
 O点为一列向右传播的简谐波的波源,如图为t=0时刻的波形,且此时波正好传播到A点.在t=5s时距x=36m的B正好第一次到达波峰.
O点为一列向右传播的简谐波的波源,如图为t=0时刻的波形,且此时波正好传播到A点.在t=5s时距x=36m的B正好第一次到达波峰.