题目内容
7.用某种单色光做双缝干涉实验时,已知双缝间距离d=0.25mm,双缝到毛玻璃屏间距离L的大小由下图中毫米刻度尺读出(如戊图所示),实验时先移动测量头(如图甲所示)上的手轮,把分划线对准靠近最左边的一条明条纹(如图乙所示),并记下螺旋测微器的读数x1(如丙图所示),然后转动手轮,把分划线向右边移动,直到对准第7条明条纹并记下螺旋测微器读数x7(如丁图所示),由以上测量数据可求该单色光的波长.图示中双缝的位置L1=100.0mm,毛玻璃屏的位置L2=938.2mm,螺旋测微器的读数x1=0.300mm,螺旋测微器读数x7=14.700mm.请用以上测量量的符号表示该单色光波长的表达式λ=$\frac{d({x}_{7}-{x}_{1})}{6({L}_{2}-{L}_{1})}$.
分析 刻度尺的读数要读到最小刻度的下一位,螺旋测微器的读数等于固定刻度读数加上可动刻度读数,需估读.根据双缝干涉条纹的间距公式求出单色光的波长.
解答 解:双缝的位置L1=100.0mm,毛玻璃屏的位置L2=938.2mm,
螺旋测微器的固定刻度读数为0.0mm,可动刻度读数为:0.01×30.0mm=0.300mm,
则螺旋测微器的读数为0.0+0.300=0.300mm;
螺旋测微器的固定刻度读数为14.5mm,可动刻度读数为:0.01×20.0mm=0.200mm,
则螺旋测微器的读数为14.5+0.200=14.700mm.
根据△x=$\frac{L}{d}$λ得:λ=$\frac{△xd}{L}$
因为L=L2-L1,△x=$\frac{{x}_{7}-{x}_{1}}{6}$,
解得:λ=$\frac{d({x}_{7}-{x}_{1})}{6({L}_{2}-{L}_{1})}$.
故答案为:100.0,938.2,0.300,14.700,$\frac{d({x}_{7}-{x}_{1})}{6({L}_{2}-{L}_{1})}$.
点评 解决本题的关键掌握刻度尺和螺旋测微器的读数方法,掌握双缝干涉条纹的间距公式,并能灵活运用.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
17. 如图所示,水平固定的直导体下方用绝缘细线悬挂一圆形线圈,直导体垂直于线圈平面,当直导体和线圈中同时通以图示电流时,线圈M的转动方向(从上往下看)以及细线中张力的变化是( )
如图所示,水平固定的直导体下方用绝缘细线悬挂一圆形线圈,直导体垂直于线圈平面,当直导体和线圈中同时通以图示电流时,线圈M的转动方向(从上往下看)以及细线中张力的变化是( )
 如图所示,水平固定的直导体下方用绝缘细线悬挂一圆形线圈,直导体垂直于线圈平面,当直导体和线圈中同时通以图示电流时,线圈M的转动方向(从上往下看)以及细线中张力的变化是( )
如图所示,水平固定的直导体下方用绝缘细线悬挂一圆形线圈,直导体垂直于线圈平面,当直导体和线圈中同时通以图示电流时,线圈M的转动方向(从上往下看)以及细线中张力的变化是( )| A. | 线圈顺时针转动,细线张力减小 | B. | 线圈逆时针转动,细线张力减小 | ||
| C. | 线圈顺时针转动,细线张力增大 | D. | 线圈逆时针转动,细线张力增大 |
15. 如图所示,工是一个带有铁芯的自感系数很大的线圈,R为一个定值电阻,两条支路的直流电阻相等.那么在闭合电键瞬间、电路稳定后和断开电键瞬间,电流表A1的读数为I1、I1′,I1″,电流表A2的读数为I2、I2′,I2″.则在三个状态下,它们大小关系分别是( )
如图所示,工是一个带有铁芯的自感系数很大的线圈,R为一个定值电阻,两条支路的直流电阻相等.那么在闭合电键瞬间、电路稳定后和断开电键瞬间,电流表A1的读数为I1、I1′,I1″,电流表A2的读数为I2、I2′,I2″.则在三个状态下,它们大小关系分别是( )
 如图所示,工是一个带有铁芯的自感系数很大的线圈,R为一个定值电阻,两条支路的直流电阻相等.那么在闭合电键瞬间、电路稳定后和断开电键瞬间,电流表A1的读数为I1、I1′,I1″,电流表A2的读数为I2、I2′,I2″.则在三个状态下,它们大小关系分别是( )
如图所示,工是一个带有铁芯的自感系数很大的线圈,R为一个定值电阻,两条支路的直流电阻相等.那么在闭合电键瞬间、电路稳定后和断开电键瞬间,电流表A1的读数为I1、I1′,I1″,电流表A2的读数为I2、I2′,I2″.则在三个状态下,它们大小关系分别是( )| A. | I1<I2,I1′=I2′,I1″=I2″ | B. | I1<I2,I1′<I2′,I1″>I2″ | ||
| C. | I1>I2,I1′=I2′,I1″<I2″ | D. | I1>I2,I1′>I2′,I1″=I2″ |
12.物体在月球表面的重力加速度是在地球表面的重力加速度的$\frac{1}{6}$,这说明了( )
| A. | 地球的半径是月球半径的6倍 | |
| B. | 地球的质量是月球质量的6倍 | |
| C. | 月球吸引地球的力是地球吸引月球的力的$\frac{1}{6}$ | |
| D. | 物体在月球表面的重力是其在地球表面的重力的$\frac{1}{6}$ |
19.引力常量的单位为( )
| A. | N.m2/kg 3 | B. | N.m2/kg 2 | C. | N.m/kg2 | D. | N.m/kg |
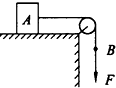 如图所示,不计绳的质量为及绳与滑轮的摩擦,物体A的质量为M,水平面光滑,当在绳B端挂一质量为m的物体时,物体A的加速度为a1,当在绳B端施以F=mg的竖直向下的拉力作用时,A的加速度为a2,则a1与a2的大小关系是( )
如图所示,不计绳的质量为及绳与滑轮的摩擦,物体A的质量为M,水平面光滑,当在绳B端挂一质量为m的物体时,物体A的加速度为a1,当在绳B端施以F=mg的竖直向下的拉力作用时,A的加速度为a2,则a1与a2的大小关系是( ) 如图所示,小木块放置于旋转的水平转台上,随转台一起匀速转动,小木块受到的摩擦力对木块做功为零,若小木块随转台一起加速转动而没有相对滑动,则小木块受到的摩擦力对木块做正功.
如图所示,小木块放置于旋转的水平转台上,随转台一起匀速转动,小木块受到的摩擦力对木块做功为零,若小木块随转台一起加速转动而没有相对滑动,则小木块受到的摩擦力对木块做正功.