1.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x},}&{x≤0}\\{lo{g}_{2}}&{x,x>0}\end{array}\right.$,若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
20.已知三棱锥P-ABC的四个顶点都在球O的球面上,若PA=AB=2,AC=1,∠BAC=120°,且PA⊥平面ABC,则球O的表面积为( )
| A. | $\frac{40π}{3}$ | B. | $\frac{50π}{3}$ | C. | 12π | D. | 15π |
19.已知锐角α满足$\sqrt{3}$sinα+cosα=$\frac{8}{5}$,则tan($α+\frac{π}{6}$)=( )
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | $±\frac{4}{3}$ | D. | $\frac{3}{4}$ |
18.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{(π+2)\sqrt{3}}{12}$ | B. | $\frac{(π+1)\sqrt{3}}{12}$ | C. | $\frac{(2π+1)\sqrt{3}}{12}$ | D. | $\frac{(2π+3)\sqrt{3}}{12}$ |
17.执行如图的程序框图,若输入的x为6,则输出的y的值为( )


| A. | 6 | B. | 4 | C. | 3 | D. | 2.5 |
16.已知点A,B是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的顶点,P为双曲线上除顶点外的一点,记kPA,kPB分别表示直线PA,PB的斜率,若kPA•kPB=$\frac{5}{4}$,则该双曲线的离心率为( )
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
15.命题“?x∈R,tanx≠1”的否定是( )
0 245183 245191 245197 245201 245207 245209 245213 245219 245221 245227 245233 245237 245239 245243 245249 245251 245257 245261 245263 245267 245269 245273 245275 245277 245278 245279 245281 245282 245283 245285 245287 245291 245293 245297 245299 245303 245309 245311 245317 245321 245323 245327 245333 245339 245341 245347 245351 245353 245359 245363 245369 245377 266669
| A. | ?x∉R,tanx≠1 | B. | ?x∈R,tanx=1 | C. | ?x∉R,tanx≠1 | D. | ?x∈R,tanx=1 |
 的定义域为
的定义域为 ,以下命题正确的是( )
,以下命题正确的是( ) 与函数
与函数 的图象关于直线
的图象关于直线 对称;
对称; 的图象既关于点
的图象既关于点 成中心对称,对于任意
成中心对称,对于任意 ,又有
,又有 ,则
,则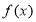 的图象关于直线
的图象关于直线 对称;
对称; ,满足关系式
,满足关系式 ,则函数
,则函数 是奇函数.
是奇函数.