题目内容
已知函数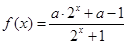 .
.
(I)求证:不论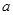 为何实数
为何实数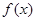 总是为增函数;
总是为增函数;
(II)确定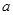 的值, 使
的值, 使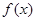 为奇函数;
为奇函数;
(Ⅲ)当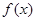 为奇函数时, 求
为奇函数时, 求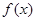 的值域.
的值域.
【答案】
(1) 见解析;(2) 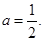
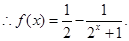 ;(3)
;(3)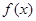 的值域为
的值域为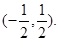
【解析】本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力与化归与转化思想.属于基础题.
(1)先设x1<x2,欲证明不论a为何实数f(x)总是为增函数,只须证明:f(x1)-f(x2)<0,即可;
(2)根据f(x)为奇函数,利用定义得出f(-x)=-f(x),从而求得a值即可;
(3)由(2)知f(x)=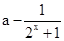 利用指数函数2x的性质结合不等式的性质即可求得f(x)的值域.
利用指数函数2x的性质结合不等式的性质即可求得f(x)的值域.
解: (1) 依题设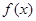 的定义域为
的定义域为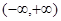 ……1分
……1分
原函数即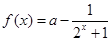 ,设
,设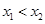 ,
,
则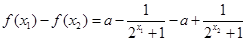 =
=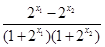 ,……2分
,……2分
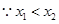 ,
, 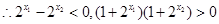 ,
,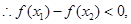
即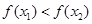 ,所以不论
,所以不论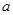 为何实数
为何实数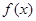 总为增函数. ……5分
总为增函数. ……5分
(2) 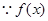 为奇函数,
为奇函数, 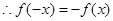 ,即
,即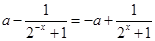 ,
,
则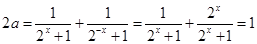 ,
,

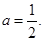
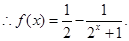 ……10分
……10分
(3)由(2)知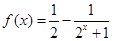 ,
, 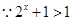 ,
, ,
,
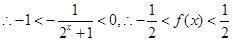
所以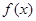 的值域为
的值域为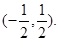 ……14分
……14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. ,,求△ABC的面积.
,,求△ABC的面积. .
. .
. .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值. .
. 的值;
的值;