题目内容
已知函数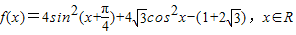 .
.(I)求函数f(x)图象的对称中心和单调递增区间;
(II)△ABC中,角A,B,C的对边分别是a,b,c,且满足a,b,c依次成等比数列,求f(B)的最值.
【答案】分析:(1)利用三角恒等变换化简函数f(x)的解析式为f(x)=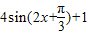 ,由此求得它的对称中心和单调增区间.
,由此求得它的对称中心和单调增区间.
(2))△ABC中,由等比数列的定义、余弦定理以及基本不等式求得cosB≥ ,从而得到B的范围,再根据正弦函数的定义域和值域求得f(B)的最值.
,从而得到B的范围,再根据正弦函数的定义域和值域求得f(B)的最值.
解答:解:(1)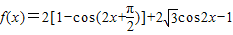 =
=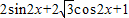 =
=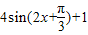 ,…(2分).
,…(2分).
令2x+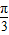 =kπ,k∈z,解得 x=
=kπ,k∈z,解得 x=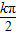 -
-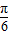 ,k∈z,
,k∈z,
故函数f(x)图象的对称中心为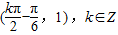 …(4分).
…(4分).
由 2kπ-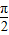 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+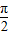 ,k∈Z,求得
,k∈Z,求得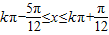 ,
,
故函数f(x)的单调递增区间为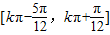 ,k∈Z…(6分).
,k∈Z…(6分).
(2))△ABC中,∵a,b,c成等比数列,∴b2=ac,
由余弦定理可得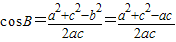
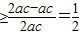 ,∴
,∴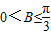 …(8分).
…(8分).
由于f(B)=4sin(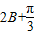 )+1,
)+1,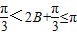 ,
,
当且仅当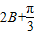 =
=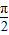 ,即
,即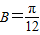 时,f(B)max=5,…(10分).
时,f(B)max=5,…(10分).
当且仅当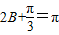 ,即
,即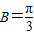 时,f(B)min=1…(12分).
时,f(B)min=1…(12分).
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的对称性、单调性、定义域和值域,等比数列的定义和性质,基本不等式的应用,属于中档题.
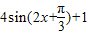 ,由此求得它的对称中心和单调增区间.
,由此求得它的对称中心和单调增区间.(2))△ABC中,由等比数列的定义、余弦定理以及基本不等式求得cosB≥
 ,从而得到B的范围,再根据正弦函数的定义域和值域求得f(B)的最值.
,从而得到B的范围,再根据正弦函数的定义域和值域求得f(B)的最值.解答:解:(1)
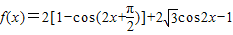 =
=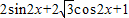 =
=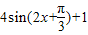 ,…(2分).
,…(2分).令2x+
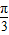 =kπ,k∈z,解得 x=
=kπ,k∈z,解得 x=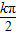 -
-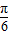 ,k∈z,
,k∈z,故函数f(x)图象的对称中心为
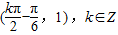 …(4分).
…(4分).由 2kπ-
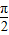 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+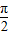 ,k∈Z,求得
,k∈Z,求得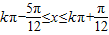 ,
,故函数f(x)的单调递增区间为
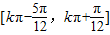 ,k∈Z…(6分).
,k∈Z…(6分).(2))△ABC中,∵a,b,c成等比数列,∴b2=ac,
由余弦定理可得
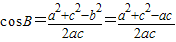
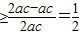 ,∴
,∴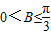 …(8分).
…(8分).由于f(B)=4sin(
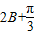 )+1,
)+1,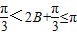 ,
,当且仅当
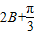 =
=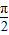 ,即
,即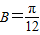 时,f(B)max=5,…(10分).
时,f(B)max=5,…(10分).当且仅当
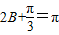 ,即
,即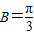 时,f(B)min=1…(12分).
时,f(B)min=1…(12分).点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的对称性、单调性、定义域和值域,等比数列的定义和性质,基本不等式的应用,属于中档题.

练习册系列答案
相关题目
 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示.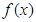 的
解 析 式;
的
解 析 式;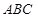 中,角
中,角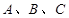 的
对 边 分 别 是
的
对 边 分 别 是 ,若
,若 的
取 值 范 围.
的
取 值 范 围.