题目内容
 已知函数f(x)=2cosx(sinx-cosx)+1.
已知函数f(x)=2cosx(sinx-cosx)+1.(1)求函数f(x)的振幅、周期、初相;
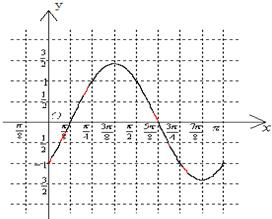
(2)画出函数y=f(x)在区间[0,π]内的图象.
(3)说明f(x)的图象可由y=sinx的图象经过怎样的变换得到.
分析:(1)根据函数f(x)=2cosx(sinx-cosx)+1,结合除幂公式(二倍角公式逆用)及和差角公式,可将函数的解析式化为y=Asin(ωx+φ)的形式,根据振幅为A,周期T=
,初相为φ,可得答案.
(2)分别令x=0,
,
,
,
,π,根据(1)中函数解析式求出函数值,描点点线可得函数y=f(x)在区间[0,π]内的图象.
(3)根据(1)中函数解析式及平移前函数解析式y=sinx,分析A,ω及φ的关键,结合y=Asin(ωx+φ)图象变换法则可得答案.
| 2π |
| ω |
(2)分别令x=0,
| π |
| 8 |
| 3π |
| 8 |
| 5π |
| 8 |
| 7π |
| 8 |
(3)根据(1)中函数解析式及平移前函数解析式y=sinx,分析A,ω及φ的关键,结合y=Asin(ωx+φ)图象变换法则可得答案.
解答:解:(1)∵f(x)=2cosx(sinx-cosx)+1
∴f(x)=2cosx(sinx-cosx)+1=sin2x-cos2x=
sin(2x-
)
即函数f(x)的振幅为
;周期为 π;初相为-
(2)列表,图象如下图示
(3)把y=sinx图象上所有点向右平移
个单位得到y=sin(x-
)的图象
再把y=sin(x-
)的图象上所有点的横坐标缩短为原来的
倍(纵坐标不变)得到y=sin(2x-
)的图象
最后把y=sin(2x-
)的图象上所有点的纵坐标伸长为原来的
倍(横坐标不变)即得y=
sin(2x-
)的图象
∴f(x)=2cosx(sinx-cosx)+1=sin2x-cos2x=
| 2 |
| π |
| 4 |
即函数f(x)的振幅为
| 2 |
| π |
| 4 |
(2)列表,图象如下图示
| x | 0 |
|
|
|
|
π | ||||||||||
2x-
|
-
|
0 |
|
π |
|
| ||||||||||
| f(x) | -1 | 0 |
|
0 | -
|
-1 |
| π |
| 4 |
| π |
| 4 |
再把y=sin(x-
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
最后把y=sin(2x-
| π |
| 4 |
| 2 |
| 2 |
| π |
| 4 |

点评:本题考查的知识点是y=Asin(ωx+φ)中参数的物理意义,五点法作函数y=Asin(ωx+φ)的图象,函数y=Asin(ωx+φ)的图象变换,是正弦函数图象和性质的综合应用,难度中等.

练习册系列答案
相关题目