题目内容
(本小题满分12分)
已知函数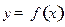 对任意的实数
对任意的实数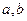 ,都有
,都有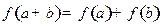 ,且当
,且当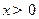 时,
时,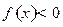
(1)求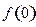 ;
;
(2)证明函数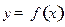 在区间
在区间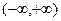 上是单调递减的函数;
上是单调递减的函数;
(3)若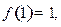 解不等式
解不等式 .
.

已知函数
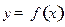 对任意的实数
对任意的实数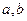 ,都有
,都有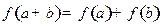 ,且当
,且当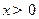 时,
时,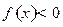
(1)求
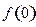 ;
;(2)证明函数
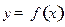 在区间
在区间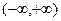 上是单调递减的函数;
上是单调递减的函数;(3)若
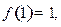 解不等式
解不等式 .
. 解:(1)令 由
由 得
得

 ……………………………………………………………………2分
……………………………………………………………………2分
(2)证明:设 且
且 ,则
,则


 …………………………………4分
…………………………………4分


由 当
当 >0时,
>0时, 得
得
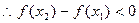 即
即
 函数
函数 在区间
在区间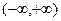 上是减函数. ……………………………7分
上是减函数. ……………………………7分

 由
由 得
得

 ……………………………………………………………………2分
……………………………………………………………………2分(2)证明:设
 且
且 ,则
,则

 …………………………………4分
…………………………………4分

由
 当
当 >0时,
>0时, 得
得
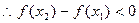 即
即
 函数
函数 在区间
在区间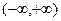 上是减函数. ……………………………7分
上是减函数. ……………………………7分
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 元(
元( )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为 元(
元( )时,一年的销售量为
)时,一年的销售量为 万件.
万件.  (万元)与每件产品的售价
(万元)与每件产品的售价
 ,若对于任意
,若对于任意 ,总存在
,总存在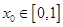 ,使得
,使得 成立,则
成立,则 的 取值范围是 ▲ .
的 取值范围是 ▲ . 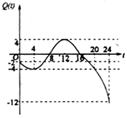
 在[0,1]上的最大值和最小值的和为3,则
在[0,1]上的最大值和最小值的和为3,则 的值是( )
的值是( )

 则
则 =" " ;
=" " ;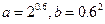 的大小(用<,>,或=表示) .
的大小(用<,>,或=表示) . 的定义域为(0,1),求函数
的定义域为(0,1),求函数 的定义域( )
的定义域( )