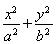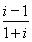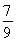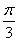题目内容
已知a＝(3，4)，b＝(4，3)，求x、y的值使(xa＋yb)⊥a，且|xa＋yb|＝1.
【解析】由a＝(3，4)，b＝(4，3)，有xa＋yb＝(3x＋4y，4x＋3y)．
(xa＋yb)⊥a?(xa＋yb)·a＝0?3(3x＋4y)＋4(4x＋3y)＝0，即25x＋24y＝0.①
又|xa＋yb|＝1?|xa＋yb|2＝1，
有(3x＋4y)2＋(4x＋3y)2＝1，
整理得25x2＋48xy＋25y2＝1，
即x(25x＋24y)＋24xy＋25y2＝1，②
由①②有24xy＋25y2＝1，③
将①变形代入③可得y＝±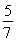
，
再代回①得
练习册系列答案
阅读快车系列答案
相关题目
