题目内容
 以O为原点,
以O为原点,| OA |
| OA |
| AG |
(1)若以O为中心,A为顶点的双曲线经过点G,求当|
| OG |
(2)过点N(0,1)能否作出直线l,使l与双曲线C交于S,T两点,且OS⊥OT?若存在,求出直线l的方程;若不存在,说明理由.
分析:(1)根据
•
=1建立等式,求出m,然后根据基本不等式求出m的最小值,从而求出点G的坐标,代入双曲线方程求出b的值即可;
(2)若存在满足条件的直线l:y=kx+1(k≠0),设S(x1,y1),T(x2,y2),OS⊥OT⇒x1x2+y1y2=0,然后将直线与双曲线联立方程组进行求解即可.
| OA |
| AG |
(2)若存在满足条件的直线l:y=kx+1(k≠0),设S(x1,y1),T(x2,y2),OS⊥OT⇒x1x2+y1y2=0,然后将直线与双曲线联立方程组进行求解即可.
解答:解:(1)
=(m-t,3),
=(t,0),
•
=t(m-t)=1⇒m=t+
≥2,t∈(0,+∞)
即t=1时,|
|取最小值,此时G(2,3),设双曲线C的方程为x2-
=1,
则4-
=1⇒b2=3,∴|
|取最小值时双曲线C的方程为x2-
=1.
(2)若存在满足条件的直线l:y=kx+1(k≠0),设S(x1,y1),T(x2,y2),OS⊥OT⇒x1x2+y1y2=0(*)
即x1x2+(kx1+1)(kx2+1)=(1+k2)x1x2+k(x1+x2)+1=0,
由
⇒(3-k2)x2-2kx-4=0由△>0⇒k2<4
又x1+x2=
,x1x2=
代入(*)得:
∴
+
+1=0⇒k2=-
⇒k∈?,即不存在满足条件的直线l.
| AG |
| OA |
| OA |
| AG |
| 1 |
| t |
即t=1时,|
| OG |
| y2 |
| b2 |
则4-
| 9 |
| b2 |
| OG |
| y2 |
| 3 |
(2)若存在满足条件的直线l:y=kx+1(k≠0),设S(x1,y1),T(x2,y2),OS⊥OT⇒x1x2+y1y2=0(*)
即x1x2+(kx1+1)(kx2+1)=(1+k2)x1x2+k(x1+x2)+1=0,
由
|
又x1+x2=
| 2k |
| 3-k2 |
| -4 |
| 3-k2 |
∴
| -4(1+k2) |
| 3-k2 |
| 2k2 |
| 3-k2 |
| 1 |
| 3 |
点评:本题主要考查了向量在几何中的应用,以及利用基本不等式的应用,属于中档题.

练习册系列答案
相关题目
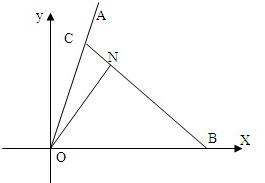 如图,一列载着危重病人的火车从O地出发,沿射线OA方向行驶,其中
如图,一列载着危重病人的火车从O地出发,沿射线OA方向行驶,其中 如图,一列载着危重病人的火车从O地出发,沿射线OA方向行驶,其中
如图,一列载着危重病人的火车从O地出发,沿射线OA方向行驶,其中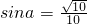 ,在距离O地5a(a为正常数)千米,北偏东β角的N处住有一位医学专家,其中
,在距离O地5a(a为正常数)千米,北偏东β角的N处住有一位医学专家,其中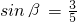 ,现120指挥中心紧急征调离O地正东p千米B处的救护车,先到N处载上医学专家,再全速赶往乘有危重病人的火车,并在C处相遇.经计算,当两车行驶的路线与OB所围成的三角形OBC面积S最小时,抢救最及时.
,现120指挥中心紧急征调离O地正东p千米B处的救护车,先到N处载上医学专家,再全速赶往乘有危重病人的火车,并在C处相遇.经计算,当两车行驶的路线与OB所围成的三角形OBC面积S最小时,抢救最及时. ,在距离O地5a(a为正常数)千米,北偏东β角的N处住有一位医学专家,其中
,在距离O地5a(a为正常数)千米,北偏东β角的N处住有一位医学专家,其中 ,现120指挥中心紧急征调离O地正东p千米B处的救护车,先到N处载上医学专家,再全速赶往乘有危重病人的火车,并在C处相遇.经计算,当两车行驶的路线与OB所围成的三角形OBC面积S最小时,抢救最及时.
,现120指挥中心紧急征调离O地正东p千米B处的救护车,先到N处载上医学专家,再全速赶往乘有危重病人的火车,并在C处相遇.经计算,当两车行驶的路线与OB所围成的三角形OBC面积S最小时,抢救最及时.