题目内容
在以O为坐标原点的直角坐标系中,| OA |
| AB |
(1) 求向量
| AB |
(2) 求圆(x-3)2+(y+1)2=10关于直线OB对称的圆的方程;
(3) 设直线l
| AB |
| x2 |
| 16 |
分析:(1)设B(x0,5),则
=(4,-3),
=(x0-4,8),由
⊥
,可得4(x0-4)-24=0,x0=10,由此能够求出向量
的坐标及OB所在的直线方程.
(2)设圆心关于直线OB的对称点坐标为(x1,y1),由(x-3)2+(y+1)2=10,可知圆心为(3,-1),半径为
.由方程y=
x知kOB=
,由此能够推导出所求圆的方程.
(3)假设椭圆上存在两点P(x1,y1),Q(x2,y2)关于直线l对称,设其中点坐标为M(x0,y0)由已知直线l的方程为y=
x+a,可设直线AB的方程为y=-
x+m,将其与已知椭圆方程联立得5x2-12mx+8m2-8=0.再由韦达定理进行求解.
| OA |
| AB |
| OA |
| AB |
| AB |
(2)设圆心关于直线OB的对称点坐标为(x1,y1),由(x-3)2+(y+1)2=10,可知圆心为(3,-1),半径为
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)假设椭圆上存在两点P(x1,y1),Q(x2,y2)关于直线l对称,设其中点坐标为M(x0,y0)由已知直线l的方程为y=
| 4 |
| 3 |
| 3 |
| 4 |
解答:解:(1)设B(x0,5),
则
=(4,-3),
=(x0-4,8),
由
⊥
,可得
•
=0,
∴4(x0-4)-24=0,x0=10,
∴B(10,5),∴
=(6,8),
OB所在的直线方程是:y=
x(5分)
(2)设圆心关于直线OB的对称点坐标为(x1,y1),
由(x-3)2+(y+1)2=10,
可知圆心为(3,-1),半径为
.
由方程y=
x知kOB=
,
∴
=-2,又点(
,
)在y=
x上
∴得
,∴
,
故所求圆的方程为(x-1)2+(y-3)2=10.(10分)
(3)假设椭圆上存在两点P(x1,y1),Q(x2,y2)关于直线l对称,
设其中点坐标为M(x0,y0),
由已知直线l的方程为y=
x+a,
可设直线AB的方程为y=-
x+m
将其与已知椭圆方程联立,
得5x2-12mx+8m2-8=0.
由韦达定理知x0=
=
,
y0=
×
+m=
.(12分)
中点M(x0,y0)在圆的内部可知
+(
)2<1,
解得m2<10.
又M(x0,y0)在直线l上,
故
=
×
+a,
解得m=-
a代入m2<10
解得a∈(-
,
),
即存在满足题意的实数a,
其取值范围为a∈(-
,
).(16分)
则
| OA |
| AB |
由
| OA |
| AB |
| OA |
| AB |
∴4(x0-4)-24=0,x0=10,
∴B(10,5),∴
| AB |
OB所在的直线方程是:y=
| 1 |
| 2 |
(2)设圆心关于直线OB的对称点坐标为(x1,y1),
由(x-3)2+(y+1)2=10,
可知圆心为(3,-1),半径为
| 10 |
由方程y=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| y1+1 |
| x1-3 |
| x1+3 |
| 2 |
| y1-1 |
| 2 |
| 1 |
| 2 |
∴得
|
|
故所求圆的方程为(x-1)2+(y-3)2=10.(10分)
(3)假设椭圆上存在两点P(x1,y1),Q(x2,y2)关于直线l对称,
设其中点坐标为M(x0,y0),
由已知直线l的方程为y=
| 4 |
| 3 |
可设直线AB的方程为y=-
| 3 |
| 4 |
将其与已知椭圆方程联立,
得5x2-12mx+8m2-8=0.
由韦达定理知x0=
| x1+x2 |
| 2 |
| 6m |
| 5 |
y0=
| -3 |
| 4 |
| 6m |
| 5 |
| m |
| 10 |
中点M(x0,y0)在圆的内部可知
(
| ||
| 16 |
| m |
| 10 |
解得m2<10.
又M(x0,y0)在直线l上,
故
| m |
| 10 |
| 4 |
| 3 |
| 6m |
| 5 |
解得m=-
| 2 |
| 3 |
解得a∈(-
| 3 |
| 2 |
| 10 |
| 3 |
| 2 |
| 10 |
即存在满足题意的实数a,
其取值范围为a∈(-
| 3 |
| 2 |
| 10 |
| 3 |
| 2 |
| 10 |
点评:本题考查圆的性质和应用,解题时要认真审题,仔细解答,注意合理地选取用公式.

练习册系列答案
相关题目
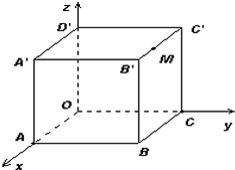 11、如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
11、如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
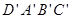 ,点M在
,点M在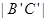 上,且
上,且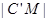
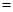 2
2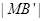 ,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 .
,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 .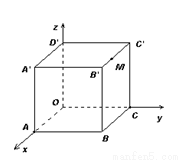
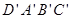 ,点M在
,点M在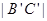 上,且
上,且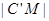
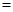 2
2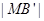 ,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
.
,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
.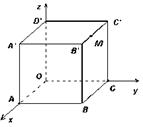
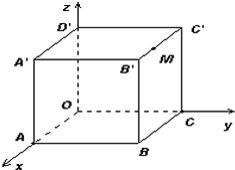 如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 ________.
如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 ________.