题目内容
已知函数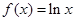 ,
,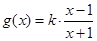
(1)求函数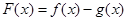 的单调区间;
的单调区间;
(2)当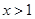 时,函数
时,函数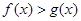 恒成立,求实数
恒成立,求实数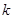 的取值范围;
的取值范围;
(3)设正实数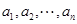 满足
满足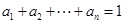 .求证:
.求证:
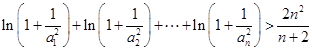 .
.
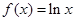 ,
,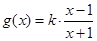
(1)求函数
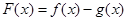 的单调区间;
的单调区间;(2)当
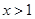 时,函数
时,函数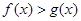 恒成立,求实数
恒成立,求实数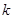 的取值范围;
的取值范围;(3)设正实数
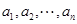 满足
满足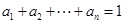 .求证:
.求证: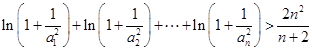 .
.(1)当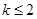 时,只有单调递增区间;
时,只有单调递增区间;
当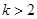 时,单调递增区间为
时,单调递增区间为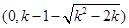 ,
,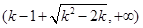 ;
;
单调递减区间为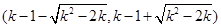
(2)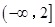
(3)由(2)知,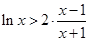 在
在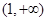 恒成立,构造函数来求证不等式。
恒成立,构造函数来求证不等式。
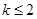 时,只有单调递增区间;
时,只有单调递增区间;当
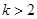 时,单调递增区间为
时,单调递增区间为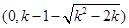 ,
,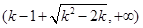 ;
;单调递减区间为
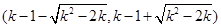
(2)
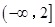
(3)由(2)知,
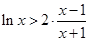 在
在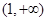 恒成立,构造函数来求证不等式。
恒成立,构造函数来求证不等式。试题分析:
1)
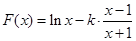
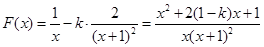 , 1分
, 1分由
 的判别式
的判别式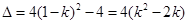 ,
,①当
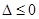 即
即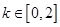 时,
时,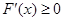 恒成立,则
恒成立,则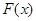 在
在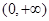 单调递增; 2分
单调递增; 2分②当
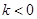 时,
时,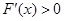 在
在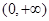 恒成立,则
恒成立,则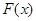 在
在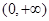 单调递增; 3分
单调递增; 3分③当
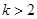 时,方程
时,方程 的两正根为
的两正根为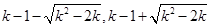
则
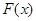 在
在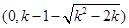 单调递增,
单调递增,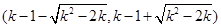 单调递减,
单调递减,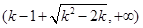 单调递增.
单调递增.综上,当
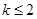 时,只有单调递增区间;
时,只有单调递增区间;当
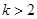 时,单调递增区间为
时,单调递增区间为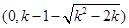 ,
,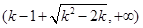 ;
;单调递减区间为
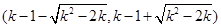 . 5分
. 5分(2)即
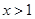 时,
时,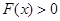 恒成立.
恒成立.当
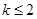 时,
时,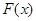 在
在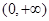 单调递增,
单调递增,∴当
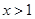 时,
时,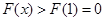 满足条件. 7分
满足条件. 7分当
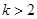 时,
时,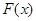 在
在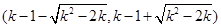 单调递减,
单调递减,则
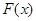 在
在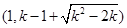 单调递减,
单调递减,此时
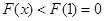 不满足条件,
不满足条件,故实数
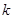 的取值范围为
的取值范围为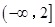 . 9分
. 9分(3)由(2)知,
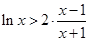 在
在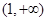 恒成立,
恒成立,令
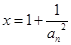 ,则
,则 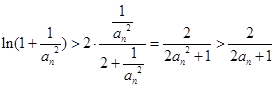 , 10分
, 10分∴
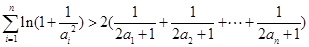 . 11分
. 11分又
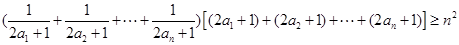 ,
,∴
 , 13分
, 13分∴
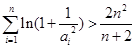 . 14分
. 14分点评:主要是考查了导数在研究函数单调性中的运用,属于基础题。

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
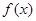 对任意的
对任意的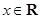 都有
都有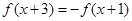 ,且
,且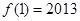 ,则
,则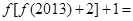 ( )
( )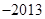
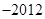
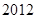
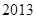
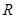 上的函数
上的函数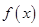 ,满足当
,满足当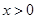 时,
时,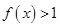 ,且对任意
,且对任意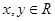 ,有
,有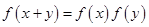 ,
,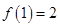
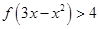
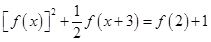
 ,曲线
,曲线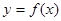 在点
在点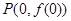 处的切线方程为
处的切线方程为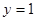
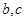 的值
的值 的三条不同切线,求
的三条不同切线,求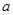 的取值范围
的取值范围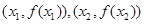 处的切线都过点(0,2),证明:当
处的切线都过点(0,2),证明:当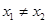 时,
时,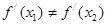
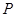 :函数
:函数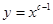 在
在 上为减函数, 命题
上为减函数, 命题 的值域为
的值域为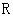 ,命题
,命题 函数
函数 定义域为
定义域为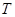 为真命题,求
为真命题,求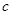 的取值范围。
的取值范围。 为真命题,
为真命题,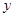 (万元)随投资收益
(万元)随投资收益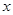 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%. 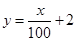 ;②
;②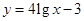 .
.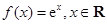 .
. 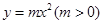 公共点的个数.
公共点的个数. 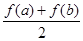 与
与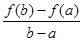 的大小, 并说明理由.
的大小, 并说明理由. 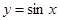 通过坐标变换公式
通过坐标变换公式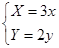 ,变换得到的新曲线为
,变换得到的新曲线为 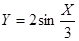
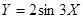

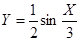
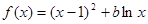 ,其中
,其中 为常数.
为常数.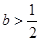 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;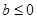 时,求
时,求 ,不等式
,不等式 都成立.
都成立.