题目内容
(本小题满分12分)已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,其左、右焦点分别是F1、F2,点P是坐标平面内的一点,且|OP|=
,其左、右焦点分别是F1、F2,点P是坐标平面内的一点,且|OP|=![]() ,
,![]() ·
·![]() =
=![]() (点O为坐标原点).
(点O为坐标原点).
(Ⅰ)求椭圆C的方程;
(Ⅱ)直线y=x与椭圆C在第一象限交于A点,若椭圆C上两点M、N使![]() +
+![]() =λ
=λ![]() ,λ∈(0,2)求△OMN面积的最大值.
,λ∈(0,2)求△OMN面积的最大值.
解:(Ⅰ)设![]()
由![]() 得
得![]() , ……1分
, ……1分
由![]() 得
得![]() ,
,
即![]() ……2分
……2分
所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ……3分
……3分
椭圆C的方程为:![]() ; ……4分
; ……4分
(Ⅱ)解法一:由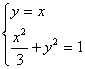 得
得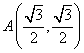 ,
,
设直线![]() 的方程为
的方程为![]() ,联立方程组
,联立方程组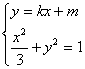
消去y得:![]() ……5分
……5分
设![]() ,
,
则![]() ……6分
……6分
![]()
∵![]() ,∴
,∴![]() ,
,![]()
得![]() ,于是
,于是![]() ……8分
……8分
![]()
![]() ……9分
……9分
![]() 到直线
到直线![]() 的距离为
的距离为![]()
∴![]() ,
,
当![]() ,即
,即![]() 时等号成立,
时等号成立,![]() 的最大值为
的最大值为![]() ……12分
……12分
解法二:由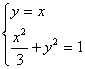 得
得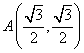 ,
,
设![]() 则
则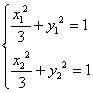
∴![]() …………① ……5分
…………① ……5分
∵![]() ,
,
∴![]() ,
,![]() 代入①得
代入①得![]() , ……6分
, ……6分
设直线![]() 的方程为
的方程为![]()
![]() ……7分
……7分
![]() 椭圆方程得
椭圆方程得 ![]()
![]() ,
,
![]() ……9分
……9分
![]() 到直线
到直线![]() 的距离为
的距离为![]()
∴![]() , ……11分
, ……11分
当![]() 时等号成立,
时等号成立,![]() 的最大值为
的最大值为![]() ……12分
……12分

练习册系列答案
相关题目