题目内容
(本小题15分)
已知函数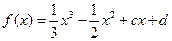 有极值.
有极值.
(1)求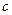 的取值范围;
的取值范围;
(2)若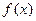 在
在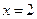 处取得极值,且当
处取得极值,且当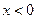 时,
时,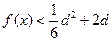 恒成立,求
恒成立,求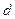 的取值范围.
的取值范围.
解:(1)∵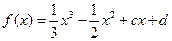 ,∴
,∴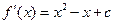 ,
,
要使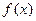 有极值,则方程
有极值,则方程 有两个实数解,
有两个实数解,
从而△=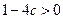 ,∴
,∴ .
.
( 2)∵
2)∵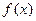 在
在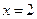 处取得极值,
处取得极值,
∴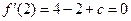 ,
,
∴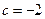 .
.
∴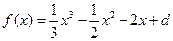 ,
,
∵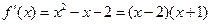 ,
,
∴当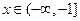 时,
时,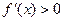 ,函数单调递增,
,函数单调递增,
当
 时,
时, ,函数单调递减.
,函数单调递减.
∴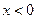 时,
时,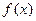 在
在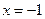 处取得最大值
处取得最大值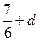 ,
,
∵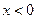 时,
时,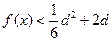 恒成立,
恒成立,
∴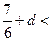
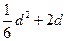 ,即
,即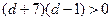 ,
,
∴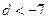 或
或 ,即
,即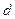 的取值范围是
的取值范围是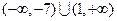 .
.
解析

练习册系列答案
相关题目
 (
(
 在
在 处有极值为
处有极值为 ,求
,求 的值;
的值; ,
, 上单调递增,求
上单调递增,求 ,
, 是实数,方程
是实数,方程 有两个实根
有两个实根 ,
, ,数列
,数列 满足
满足 ,
, ,
,
 ,
, ,求
,求 项和.
项和. ,过点
,过点 的直线
的直线 交抛物线
交抛物线 于
于 两点,且
两点,且 .
. 作
作 轴的平行线与直线
轴的平行线与直线 相交于点
相交于点 ,若
,若 是等腰三角形,求直线
是等腰三角形,求直线 的方程.
的方程. 时,不等式f(x)<m恒成立,求实数m的值;
时,不等式f(x)<m恒成立,求实数m的值;