题目内容
（本小题15分）已知函数
（
（1）若函数
在
处有极值为
，求
的值；
（2）若对任意
，在
上单调递增，求的最小值．
（15分）（1）
则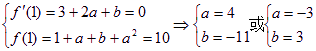
…………5分
当
时，
，所以函数有极值点；
当
，所以函数无极值点；
则
的值为
．……………………………………7分[来源:学&科&网Z&X&X&K]
（2）解法一：
对任意的
，
都成立
则
对任意的，都成立
所以得
对任意的恒成立，
即
，又
，当
时
，得
所以 的最小值为
． …………15分[来源:学科网]
解法二：对任意的，都成立
即
对任意的，都成立,
即
.令
①当
；
②当
.
又∵
,∴
.
综上，的最小值为．………15分
解析:
略
练习册系列答案
相关题目
（
在
处有极值为
，求
的值；
，
上单调递增，求
，
是实数，方程
有两个实根
，
，数列
满足
，
，
，
，求
项和．
，过点
的直线
交抛物线
于
两点，且
．
作
轴的平行线与直线
相交于点
，若
是等腰三角形，求直线
的方程．
时，不等式f(x)＜m恒成立，求实数m的值；