题目内容
已知圆M的圆心在直线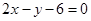 上,且过点
上,且过点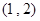 、
、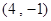 .
.
(1)求圆M的方程;
(2)设P为圆M上任一点,过点P向圆O: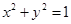 引切线,切点为Q.试探究:
引切线,切点为Q.试探究:
平面内是否存在一定点R,使得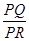 为定值?若存在,求出点R的坐标;若不存在,请说
为定值?若存在,求出点R的坐标;若不存在,请说
明理由.
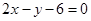 上,且过点
上,且过点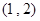 、
、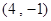 .
.(1)求圆M的方程;
(2)设P为圆M上任一点,过点P向圆O:
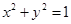 引切线,切点为Q.试探究:
引切线,切点为Q.试探究:平面内是否存在一定点R,使得
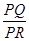 为定值?若存在,求出点R的坐标;若不存在,请说
为定值?若存在,求出点R的坐标;若不存在,请说明理由.
(1)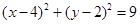 ,(2)存在点
,(2)存在点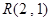 或
或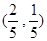 满足题意.
满足题意.
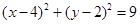 ,(2)存在点
,(2)存在点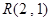 或
或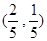 满足题意.
满足题意.试题分析:(1)求圆的标准方程,关键在于确定圆心.圆心必在两点
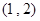 、
、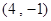 连线段的中垂线:
连线段的中垂线: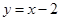 上,又在直线
上,又在直线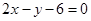 上,所以圆心为
上,所以圆心为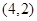 ,半径为
,半径为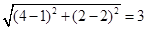 ,因此圆方程为
,因此圆方程为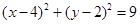 ,(2)存在性问题,一般从假设存在出发,将存在是否转化为对应方程是否有解. 设
,(2)存在性问题,一般从假设存在出发,将存在是否转化为对应方程是否有解. 设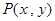 ,
,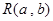 ,则
,则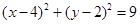 ,即
,即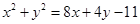 ,又
,又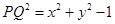 ,
,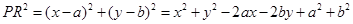 ,故
,故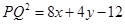 ,
,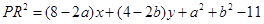 ,又设
,又设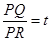 为定值,故
为定值,故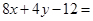
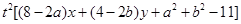 ,可得
,可得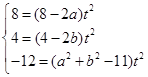 ,解得
,解得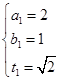 或
或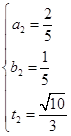 综上,存在点
综上,存在点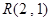 或
或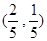 满足题意.
满足题意.试题解析:解:(1)圆M:
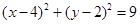 ;
;(2)设
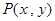 ,
,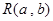 ,则
,则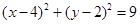 ,即
,即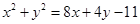 ,
,又
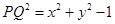 ,
,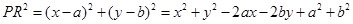 ,
,故
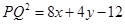 ,
,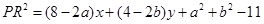 ,
,又设
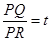 为定值,故
为定值,故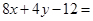
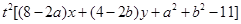 ,
,可得
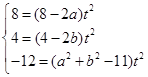 ,解得
,解得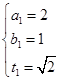 或
或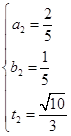 ,
,综上,存在点
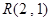 或
或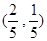 满足题意.
满足题意.
练习册系列答案
相关题目
 为圆
为圆 :
: 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为 ,则四边形
,则四边形 的面积的最大值为 .
的面积的最大值为 .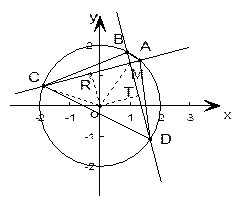
 2=1
2=1 2+(y-1)2=1
2+(y-1)2=1 ,则以
,则以 为直径的圆的标准方程为___________________.
为直径的圆的标准方程为___________________. 相切,且圆心C在直线
相切,且圆心C在直线 上.
上. 的直线l与圆C相交于A,B两点, 且
的直线l与圆C相交于A,B两点, 且 , 求直线l的方程.
, 求直线l的方程.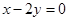 上的圆
上的圆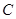 与
与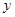 轴的正半轴相切,圆
轴的正半轴相切,圆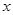 轴所得弦的长为
轴所得弦的长为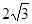 ,则圆
,则圆 关于原点对称的圆的方程是 ____ .
关于原点对称的圆的方程是 ____ .