题目内容
(1)已知不等式ax2+bx-2>0的解集是{x|-2<x<-
},求a,b的值;
(2)若关于x的一元二次方程x2-mx+m+3=0有两个不相等的实数根,求m的取值范围.
| 1 | 4 |
(2)若关于x的一元二次方程x2-mx+m+3=0有两个不相等的实数根,求m的取值范围.
分析:(1)依题意知-2,-
是方程ax2+bx-2=0的两个根,利用韦达定理,可求a,b的值;
(2)利用根的判别式大于0,可求m的取值范围.
| 1 |
| 4 |
(2)利用根的判别式大于0,可求m的取值范围.
解答:解:(1)依题意知-2,-
是方程ax2+bx-2=0的两个根-------(2分)
(2)依题意,△=m2-4(m+3)>0
∴m<-2或m>6.
| 1 |
| 4 |
|
(2)依题意,△=m2-4(m+3)>0
∴m<-2或m>6.
点评:本题考查一元二次不等式的运用,考查韦达定理,考查学生的计算能力,属于中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
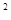 +bx+1<0的解集为{x|-1<x<2},则ab=
+bx+1<0的解集为{x|-1<x<2},则ab=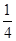 C.-
C.- D.1
D.1