题目内容
(本小题满分12分)已知函数 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)若 是第二象限角,
是第二象限角, ,求
,求 的值.
的值.
(1) ;(2)
;(2)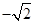 ,
,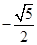 .
.
解析试题分析:(1)将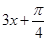 看作一个整体,根据正弦函数
看作一个整体,根据正弦函数 的单调递增区间便可得
的单调递增区间便可得 的单调递增区间.(2)将
的单调递增区间.(2)将 代入
代入 得
得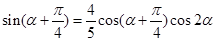 .求三角函数值时,首先考虑统一角,故利用和角公式和倍角公式化为单角
.求三角函数值时,首先考虑统一角,故利用和角公式和倍角公式化为单角 的三角函数得:
的三角函数得: .注意这里不能将
.注意这里不能将 约了.接下来分
约了.接下来分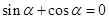 和
和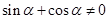 两种情况求值.
两种情况求值.
试题解析:(1)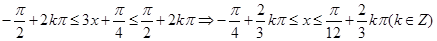 ;
;
(2)由题设得: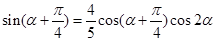 ,
,
即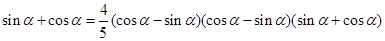 ,.
,.
若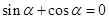 ,则
,则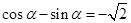 ,
,
若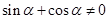 ,则
,则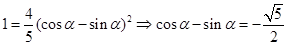 .
.
综上得, 的值为
的值为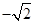 或
或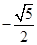 .
.
【考点定位】三角函数的性质、三角恒等变换及三角函数的求值.

练习册系列答案
相关题目
 ,则
,则 .
.  .
. ,求
,求 的值.
的值.
 写成
写成 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标; 满足
满足 ,且边
,且边 所对的角为
所对的角为 ,试求
,试求 +
+ sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
 ,且x0∈(-
,且x0∈(- ,
, ),求f(x0+1)的值.
),求f(x0+1)的值. <α<π,0<β<
<α<π,0<β< ,cos(β-α)=
,cos(β-α)= ,求sinβ的值.
,求sinβ的值. ,
, 的值.
的值. ,则
,则