题目内容
4、正方体AC1中M是棱D1D的中点,O是正方形ABCD的中心,则异面直线OA1与AM所成的角是( )
分析: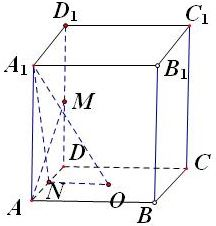 先画图,本题构造了平面A1NO,证明直线垂直平面A1NO,利用线面垂直的判定定理进行证明,再根据线面垂直的性质可知直线与面中的任一直线垂直,即可求得所成角.
先画图,本题构造了平面A1NO,证明直线垂直平面A1NO,利用线面垂直的判定定理进行证明,再根据线面垂直的性质可知直线与面中的任一直线垂直,即可求得所成角.
 先画图,本题构造了平面A1NO,证明直线垂直平面A1NO,利用线面垂直的判定定理进行证明,再根据线面垂直的性质可知直线与面中的任一直线垂直,即可求得所成角.
先画图,本题构造了平面A1NO,证明直线垂直平面A1NO,利用线面垂直的判定定理进行证明,再根据线面垂直的性质可知直线与面中的任一直线垂直,即可求得所成角.解答: 解:如图:
解:如图:
取AD的中点N,连接NO、A1N、AM
由Rt△A1NA≌Rt△AMD,∠A1NA=∠AMD
得A1N⊥AM,ON⊥AM,A1N∩ON=N
∴AM⊥面A1NO而A1O?面A1NO,即AM⊥A1O
故选A
 解:如图:
解:如图:取AD的中点N,连接NO、A1N、AM
由Rt△A1NA≌Rt△AMD,∠A1NA=∠AMD
得A1N⊥AM,ON⊥AM,A1N∩ON=N
∴AM⊥面A1NO而A1O?面A1NO,即AM⊥A1O
故选A
点评:本题主要考查了异面直线及其所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
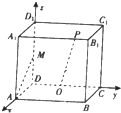 如图所示,在正方体AC1中,M是棱DD1的中点,O是平面ABCD的中心,P是A1B1上的任意一点,则直线AM与OP所成角是
如图所示,在正方体AC1中,M是棱DD1的中点,O是平面ABCD的中心,P是A1B1上的任意一点,则直线AM与OP所成角是