题目内容
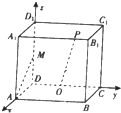如图所示，在正方体AC1中，M是棱DD1的中点，O是平面ABCD的中心，P是A1B1上的任意一点，则直线AM与OP所成角是分析：建立空间直角坐标系，给出A、M、O、P的坐标，再求出向量
，
的坐标，利用坐标运算求解即可．
| AM |
| OP |
解答：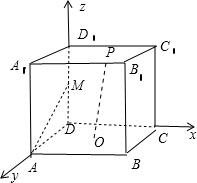
解：设正方体的棱长为2a，建立如图所示的空间坐标系，则有A（2a，0，0），M（0，0，a），O（a，a，0）
∵P是A1B1上任意一点，不妨设P（2a，m，2a）（0≤m≤2a）．
∴
=(0，0，a)-(2a，0，0)=(-2a，0，a)．
∴
=(2a，m，2a)-(a，a，0)=(a，m-a，2a)，
∴
?
=-2a×a+0×(m-a)+a×2a=0．
∴异面直线AM与OP所成角为
．
故答案是
．
解：设正方体的棱长为2a，建立如图所示的空间坐标系，则有A（2a，0，0），M（0，0，a），O（a，a，0）∵P是A1B1上任意一点，不妨设P（2a，m，2a）（0≤m≤2a）．
∴
| AM |
∴
| OP |
∴
| AM |
| OP |
∴异面直线AM与OP所成角为
| π |
| 2 |
故答案是
| π |
| 2 |
点评：本题考查异面直线所成的角，利用向量坐标运算是解决此类题的常用方法．此题也可利用证明线面垂直求解．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
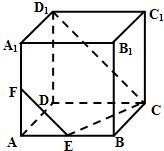如图所示，在正方体ABCD-A1B1C1D1中，E为AB的中点
（2011•宝山区二模）如图所示，在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等，则动点P所在曲线形状为（ ）
如图所示，在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等，则动点P所在曲线的形状为（ ）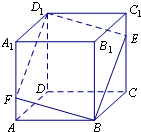
如图所示，在正方体ABCD-A1B1C1D1中，点E是棱CC1上的一个动点，平面BED1交棱AA1于点F．则下列命题中假命题是（ ）