题目内容
已知命题P:曲线y=x2+(m-1)x+1与x轴交于不同的两点,命题q:方程
+
=1表示焦点在y轴上的椭圆,若p∧q为假命题,p∨q为真命题,求实数m的取值范围.
| x2 |
| m2+1 |
| y2 |
| (m-1)2 |
分析:命题p正确,由△>0可求得m的取值范围;命题q正确,亦可求得实数m的取值范围,利用p∧q为假命题,p∨q为真命题即可求得答案.
解答:解:∵命题P:曲线y=x2+(m-1)x+1与x轴交于不同的两点,
∴△=(m-1)2-4=m2-2m-3>0,
∴m>3或m<-1;
∵命题q:
+
=1表示焦点在y轴上的椭圆,
∴(m-1)2>m2+1,
∴m<0.
∵p∧q为假命题,p∨q为真命题,
∴p真q假,或p假q真.
即
或
,
∴m>3或-1≤m<0.
∴实数m的取值范围为[-1,0)∪(3,+∞).
∴△=(m-1)2-4=m2-2m-3>0,
∴m>3或m<-1;
∵命题q:
| x2 |
| m2+1 |
| y2 |
| (m-1)2 |
∴(m-1)2>m2+1,
∴m<0.
∵p∧q为假命题,p∨q为真命题,
∴p真q假,或p假q真.
即
|
|
∴m>3或-1≤m<0.
∴实数m的取值范围为[-1,0)∪(3,+∞).
点评:本题考查复合命题的真假,分别求得命题p正确时实数m的取值范围与命题q正确时实数m的取值范围是关键,也是难点,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
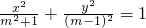 表示焦点在y轴上的椭圆,若p∧q为假命题,p∨q为真命题,求实数m的取值范围.
表示焦点在y轴上的椭圆,若p∧q为假命题,p∨q为真命题,求实数m的取值范围.