题目内容
已知命题p:曲线方程
+
=1表示焦点在y轴的双曲线;
命题q:已知
=(x,-k,1),
=(x,x,k+3),对任意x∈R,
•
>0恒成立.
(Ⅰ) 写出命题q的否定形式¬q;
(Ⅱ) 求证:命题p成立是命题q成立的充分不必要条件.
| x2 |
| 2-k |
| y2 |
| 5-k |
命题q:已知
| a |
| b |
| a |
| b |
(Ⅰ) 写出命题q的否定形式¬q;
(Ⅱ) 求证:命题p成立是命题q成立的充分不必要条件.
分析:(Ⅰ) 根据全称命题的否定是特称命题得到命题q的否定形式?q;
(Ⅱ) 根据充分条件和必要条件的定义进行证明即可.
(Ⅱ) 根据充分条件和必要条件的定义进行证明即可.
解答:解:(Ⅰ)¬q:已知
=(x,-k,1),
=(x,x,k+3),?x∈R,
•
≤0.
(Ⅱ)若曲线方程
+
=1表示焦点在y轴的双曲线,
则
,
即
,
∴2<k<5.即p:2<k<5.
若q成立,则
•
=x2-kx+k+3>0恒成立,
即△=k2-4k-12<0,
解得-2<k<6,
∵(2,5)⊆(-2,6),且(2,5)?(-2,6),
∴命题p成立是命题q成立的充分不必要条件.
| a |
| b |
| a |
| b |
(Ⅱ)若曲线方程
| x2 |
| 2-k |
| y2 |
| 5-k |
则
|
即
|
∴2<k<5.即p:2<k<5.
若q成立,则
| a |
| b |
即△=k2-4k-12<0,
解得-2<k<6,
∵(2,5)⊆(-2,6),且(2,5)?(-2,6),
∴命题p成立是命题q成立的充分不必要条件.
点评:本题主要考查含有量词的命题的否定以及充分条件和必要条件的应用,比较基础.

练习册系列答案
相关题目
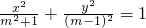 表示焦点在y轴上的椭圆,若p∧q为假命题,p∨q为真命题,求实数m的取值范围.
表示焦点在y轴上的椭圆,若p∧q为假命题,p∨q为真命题,求实数m的取值范围.