题目内容
(本小题满分12分)已知数列{an}满足a1=1,an>0,Sn是数列{an}的前n项和,对任意n∈N+,有2Sn=p(2 +an-1)(p为常数).
+an-1)(p为常数).
(1)求p和a2,a3的值;
(2)求数列{an}的通项公式.
【答案】
(1)a2= ;a3=2.(2) an=
;a3=2.(2) an=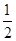 (n+1).
(n+1).
【解析】(1)令n=1,根据a1=S1=1,得到p=1,
再令n=2可得2S2=2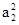 +a2-1=2(1+a2),从而可得a2的值.同理令n=3,可求出a3的值.
+a2-1=2(1+a2),从而可得a2的值.同理令n=3,可求出a3的值.
(2) 由2Sn=2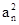 +an-1,得2Sn-1=2
+an-1,得2Sn-1=2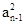 +an-1-1(n≥2),
+an-1-1(n≥2),
两式相减,得2an=2(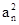 -
-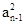 )+an-an-1,
)+an-an-1,
即(an+an-1)(2an-2an-1-1)=0,
因为an>0,所以2an-2an-1-1=0,
即an-an-1=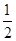 (n≥2),到此可确定{an}是等差数列,问题得解.
(n≥2),到此可确定{an}是等差数列,问题得解.
(1)令n=1得2S1=p(2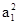 +a1-1),
+a1-1),
又a1=S1=1,得p=1;
令n=2得2S2=2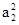 +a2-1,又S2=1+a2,
+a2-1,又S2=1+a2,
得2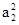 -a2-3=0, a2=
-a2-3=0, a2= 或a2=-1(舍去),
或a2=-1(舍去),
∴a2= ;
;
令n=3得2S3=2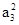 +a3-1,又S3=
+a3-1,又S3=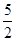 +a3,得
+a3,得
2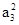 -a3-6=0,a3=2或a3=-
-a3-6=0,a3=2或a3=- (舍去),∴a3=2.
(舍去),∴a3=2.
(2)由2Sn=2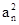 +an-1,得
+an-1,得
2Sn-1=2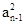 +an-1-1(n≥2),
+an-1-1(n≥2),
两式相减,得2an=2(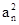 -
-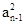 )+an-an-1,
)+an-an-1,
即(an+an-1)(2an-2an-1-1)=0,
因为an>0,所以2an-2an-1-1=0,
即an-an-1=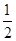 (n≥2),
(n≥2),
故{an}是首项为1,公差为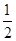 的等差数列,
的等差数列,
得an=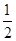 (n+1).
(n+1).

练习册系列答案
相关题目