题目内容
如图,正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F 是棱CD上的动点.
(Ⅰ)试确定点F的位置,使得D1E⊥平面AB1F;
(Ⅱ)当D1E⊥平面AB1F时,求二面角C1-EF-A的余弦值以及BA1与面C1EF所成的角的大小.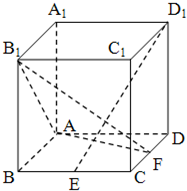
(Ⅰ)试确定点F的位置,使得D1E⊥平面AB1F;
(Ⅱ)当D1E⊥平面AB1F时,求二面角C1-EF-A的余弦值以及BA1与面C1EF所成的角的大小.

(I)由题意可得:以A为原点,分别以直线AB、AD、AA1为x轴、y轴、z轴建立空间直角坐标系,不妨设正方体的棱长为1,且DF=x,则A1(0,0,1),A(0,0,0),B(1,0,0),D(0,1,0),B1(1,0,1),D1(0,1,1),E(1,
,0),F(x,1,0)
所以
=(1,-
,-1),
=(1,0,1),
=(x,1,0)
由D1E⊥面AB1F?
⊥
且
⊥
,
所以
,可解得x=
所以当点F是CD的中点时,D1E⊥平面AB1F.
(II)当D1E⊥平面AB1F时,F是CD的中点,F(
,1,0)
由正方体的结构特征可得:平面AEF的一个法向量为
=(0,0,1),
设平面C1EF的一个法向量为
=(x,y,z),
在平面C1EF中,
=(0,
,1),
=(-
,
,0),
所以
,即
,
所以取平面C1EF的一个法向量为
=(2,2,-1),
所以cos<
,
>=-
,
所以<
,
>=π-arccos
,
又因为当把
,
都移向这个二面角内一点时,
背向平面AEF,而
指向平面C1EF,
所以二面角C1-EF-A的大小为π-arccos
又因为
=(-1,0,1),
所以cos<
,
>=-
,
所以<
,
>=135?,
∴BA1与平面C1EF所成的角的大小为45°.
| 1 |
| 2 |
所以
| D1E |
| 1 |
| 2 |
| AB1 |
| AF |
由D1E⊥面AB1F?
| D1E |
| AB1 |
| D1E |
| AF |
所以
|
| 1 |
| 2 |
所以当点F是CD的中点时,D1E⊥平面AB1F.
(II)当D1E⊥平面AB1F时,F是CD的中点,F(
| 1 |
| 2 |
由正方体的结构特征可得:平面AEF的一个法向量为
| m |
设平面C1EF的一个法向量为
| n |
在平面C1EF中,
| EC1 |
| 1 |
| 2 |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
所以
|
|
所以取平面C1EF的一个法向量为
| n |
所以cos<
| m |
| n |
| 1 |
| 3 |
所以<
| m |
| n |
| 1 |
| 3 |
又因为当把
| m |
| n |
| m |
| n |
所以二面角C1-EF-A的大小为π-arccos
| 1 |
| 3 |
又因为
| BA1 |
所以cos<
| BA1 |
| n |
| ||
| 2 |
所以<
| BA1 |
| n |
∴BA1与平面C1EF所成的角的大小为45°.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目

 如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量
如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量 如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.
如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG. 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( ) 如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且
如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且