题目内容
如图，正方体ABCD-A1B1C1D1棱长为8，E、F分别为AD1，CD1中点，G、H分别为棱DA，DC上动点，且EH⊥FG．（1）求GH长的取值范围；
（2）当GH取得最小值时，求证：EH与FG共面；并求出此时EH与FG的交点P到直线B1B的距离．
分析：（1）以D为原点，建立如图所示空间直角坐标系，设DG=a，DH=b可得E、F、G、H各点的坐标，得到
、
坐标，根据
•
=0，解出b=4-a，根据距离公式得到GH=
=
，结合二次函数的性质即可得到GH长的取值范围；
（2）由（1）知当a=b=2时，GH取得最小值．由此算出EF∥GH，即EH与FG共面，得
=(-
，
， -
)，设P（x1，y1，z1），得到
=（x1-4，y，z1-4），从而建立关于x1、y1、z1的方程组，解之得P在ABCD平面上的射影M的坐标，结合两点间的距离公式即可算出P到直线B1B的距离．
| EH |
| FG |
| EH |
| FG |
| a2+b2 |
| 2(a-2)2+8 |
（2）由（1）知当a=b=2时，GH取得最小值．由此算出EF∥GH，即EH与FG共面，得
| EP |
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| EP |
解答：解：（1）以D为原点，DA、DC、DD1分别为x轴、y轴、z轴建立空间直角坐标系．
设DG=a，DH=b，可得
E（4，0，4），F（0，4，4），G（a，0，0），H（0，b，0）．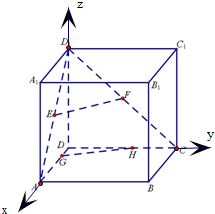
∴
=（-4，b，-4），
=（a，-4，-4）．
∵EH⊥FG，∴
•
=-4a-4b+16=0，则a+b=4，即b=4-a．
又G1H在棱DA，DC上，则0≤a≤8，0≤b≤8，从而0≤a≤4．
∴GH=
=
=
．
∴GH取值范围是[2
，4]． …（6分）
（2）当GH=2
时，a=2，b=2．
∴
=（-2，2，0），
=（-4，4，0），即
=2
．
∴EF∥GH，即EH与FG共面．
所以EF=2GH，EF∥GH，则
=
=(-
，
， -
)．
设P（x1，y1，z1），则
=（x1-4，y，z1-4）．
∴x1=
，y1=
，z1=
，即P（
，
，
）．
则P（
，
，
）在底面上ABCD上的射影为M（
，
，0）．
又∵B（8，8，0），
∴|MB|=
=
，即为点P到直线B1B的距离．…（12分）
设DG=a，DH=b，可得
E（4，0，4），F（0，4，4），G（a，0，0），H（0，b，0）．
∴
| EH |
| FG |
∵EH⊥FG，∴
| EH |
| FG |
又G1H在棱DA，DC上，则0≤a≤8，0≤b≤8，从而0≤a≤4．
∴GH=
| a2+b2 |
| a2+(4-a)2 |
| 2(a-2)2+8 |
∴GH取值范围是[2
| 2 |
（2）当GH=2
| 2 |
∴
| GH |
| EF |
| EF |
| GH |
∴EF∥GH，即EH与FG共面．
所以EF=2GH，EF∥GH，则
| EP |
| 2 |
| 3 |
| EH |
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
设P（x1，y1，z1），则
| EP |
∴x1=
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
则P（
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
又∵B（8，8，0），
∴|MB|=
(8-
|
| 20 |
| 3 |
| 2 |
点评：本题在正方体中求点到直线的距离，着重考查了空间直角坐标系的建立、利用空间向量的方法求点线距离和正方体的性质等知识，考查了空间想象能力和计算能力，属于中档题．
练习册系列答案
考前必练系列答案
相关题目
如图，正方体ABCD-A1B1C1D1中，E，F分别为BB1和A1D1的中点．证明：向量
如图，正方体ABCD-A1B1C1D1中，若E、F、G分别为棱BC、C1C、B1C1的中点，O1、O2分别为四边形ADD1A1、A1B1C1D1的中心，则下列各组中的四个点不在同一个平面上的是（ ）
如图，正方体ABCD-A1B1C1D1中，E、F、G、H分别是所在棱的三等分点，且