题目内容
 如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且BF=DE=C1G=C1H=
如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且BF=DE=C1G=C1H=| 1 | 3 |
(1)证明:直线EH与FG共面;
(2)若正方体的棱长为3,求几何体GHC1-EFC的体积.
分析:(1)先证EF∥GH,从而证明EF,GH共面,即EH,FG共面;
(2)先证明EH、FG、CC1交于一点,即证明几何体GHC1-EFC为棱台,再代入棱台的体积公式计算.
(2)先证明EH、FG、CC1交于一点,即证明几何体GHC1-EFC为棱台,再代入棱台的体积公式计算.
解答: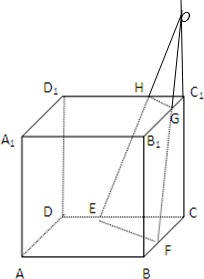 解:(1)证明:连接BD、B1D1,∵C1H=C1G,∴
解:(1)证明:连接BD、B1D1,∵C1H=C1G,∴
=
,∴HG∥D1B1
同理,由BF=DE,可得EF∥DB,又D1B1∥BD,∴HG∥EF.
∴HG、EF在平面EFHG中,由EH?平面EFHG,FG?平面EFHG,
∴直线EH与FG共面.
(2)由(1)知EH与FG共面不平行,设EH∩FG=0,
∵平面BCB1C1∩平面DCC1D1=CC1,∴O∈CC1,即EH、FG、CC1交于一点,
∴几何体GHC1-EFC为三棱台.
C1G=C1H=1,CE=CF=2,CC1=3,S1=
,S2=2,
∴V=
×(
+
+2)×3=
.
 解:(1)证明:连接BD、B1D1,∵C1H=C1G,∴
解:(1)证明:连接BD、B1D1,∵C1H=C1G,∴| C1H |
| HD1 |
| C1G |
| GB1 |
同理,由BF=DE,可得EF∥DB,又D1B1∥BD,∴HG∥EF.
∴HG、EF在平面EFHG中,由EH?平面EFHG,FG?平面EFHG,
∴直线EH与FG共面.
(2)由(1)知EH与FG共面不平行,设EH∩FG=0,
∵平面BCB1C1∩平面DCC1D1=CC1,∴O∈CC1,即EH、FG、CC1交于一点,
∴几何体GHC1-EFC为三棱台.
C1G=C1H=1,CE=CF=2,CC1=3,S1=
| 1 |
| 2 |
∴V=
| 1 |
| 3 |
| 1 |
| 2 |
|
| 7 |
| 2 |
点评:本题主要考查了棱台的性质及棱台的体积计算,考查了线共面及线共点问题,要注意棱台是由棱锥用平行于底面的平面截得的,这一性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

 如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量
如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量 如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.
如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG. 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )