题目内容
2．设Sn是等差数列{an}的前n项和，若S9=45，则a5=5．分析 由等差数列的求和公式和性质可得S9=9a5=45，解方程可得．
解答 解：由等差数列的求和公式和性质可得：
S9=$\frac{9（{a}_{1}+{a}_{9}）}{2}$=$\frac{9×2{a}_{5}}{2}$=9a5=45，
∴a5=5
故答案为：5
点评 本题考查等差数列的求和公式和性质，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
13．执行右边的程序框图，则输出的结果是（ ）
| A． | $\frac{3}{7}$ | B． | $\frac{4}{9}$ | C． | $\frac{5}{11}$ | D． | $\frac{6}{13}$ |
14．对任意非零实数a、b，若a?b的运算原理如图所示，则log24?（$\frac{1}{3}$）-1的值为（ ）
| A． | $\frac{1}{3}$ | B． | 1 | C． | $\frac{4}{3}$ | D． | 2 |
17．在复平面内，复数$\frac{2-3i}{i^3}$对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
7．把函数$y=5sin（2x-\frac{π}{6}）$图象上所有点的横坐标伸长为原来的2倍（纵坐标不变），再把所得函数的图象向右平移$\frac{π}{3}$个单位，得到图象的解析式为（ ）
| A． | y=5cosx | B． | y=5cos4x | C． | y=-5cosx | D． | y=-5 cos4x |
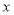（吨）与相应的生产能耗
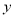（吨标准煤）的几组对应数据，根据表中提供的数据，求出
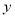关于
的线性回归方程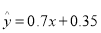
，那么表中
的值为？（ ）