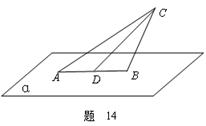
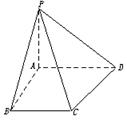
题目内容
如图,在梯形ABCD中,AD∥BC,∠ABC=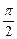 ,AB=
,AB=  AD=a,
AD=a,
∠ADC=arccos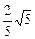 ,PA⊥面ABCD且PA=a.
,PA⊥面ABCD且PA=a.
(1)求异面直线AD与PC间的距离;
(2)在线段AD上是否存在一点F,使点A到平面PCF的距离为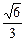
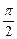 ,AB=
,AB=  AD=a,
AD=a,∠ADC=arccos
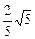 ,PA⊥面ABCD且PA=a.
,PA⊥面ABCD且PA=a.(1)求异面直线AD与PC间的距离;
(2)在线段AD上是否存在一点F,使点A到平面PCF的距离为
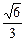

(1)AE= a (2)在AD上存在满足条件的点F.
a (2)在AD上存在满足条件的点F.
 a (2)在AD上存在满足条件的点F.
a (2)在AD上存在满足条件的点F.(1)∵BC∥AD,BC 面PBC,∴AD∥面PBC
面PBC,∴AD∥面PBC
从而AD与PC间的距离就是直线AD与平面PBC间的距离.
过A作AE⊥PB,又AE⊥BC
∴AE⊥平面PBC,AE为所求.
在等腰直角三角形PAB中,PA=AB=a
∴AE= a
a
(2)作CM∥AB,由已知cosADC=
∴tanADC= ,即CM=
,即CM= DM
DM
∴ABCM为正方形,AC= a,PC=
a,PC= a
a
过A作AH⊥PC,在Rt△PAC中,得AH=
下面在AD上找一点F,使PC⊥CF
取MD中点F,△ACM、△FCM均为等腰直角三角形
∴∠ACM+∠FCM=45°+45°=90°
∴FC⊥AC,即FC⊥PC∴在AD上存在满足条件的点F.
 面PBC,∴AD∥面PBC
面PBC,∴AD∥面PBC从而AD与PC间的距离就是直线AD与平面PBC间的距离.
过A作AE⊥PB,又AE⊥BC
∴AE⊥平面PBC,AE为所求.
在等腰直角三角形PAB中,PA=AB=a
∴AE=
 a
a(2)作CM∥AB,由已知cosADC=

∴tanADC=
 ,即CM=
,即CM= DM
DM∴ABCM为正方形,AC=
 a,PC=
a,PC= a
a过A作AH⊥PC,在Rt△PAC中,得AH=

下面在AD上找一点F,使PC⊥CF
取MD中点F,△ACM、△FCM均为等腰直角三角形
∴∠ACM+∠FCM=45°+45°=90°
∴FC⊥AC,即FC⊥PC∴在AD上存在满足条件的点F.

练习册系列答案
相关题目
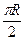 ,则这两点的球面距离是 ( )
,则这两点的球面距离是 ( )


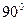 ,点D1、F1分别是A1B1、A1C1的中点,BC=CA=CC1,则BD1与AF1所成角的余弦值是( )
,点D1、F1分别是A1B1、A1C1的中点,BC=CA=CC1,则BD1与AF1所成角的余弦值是( ) 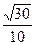
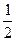

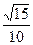
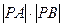 最小。
最小。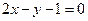 和
和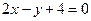 间的距离为
间的距离为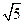
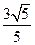
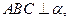
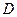 为
为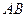 的中点,
的中点,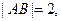
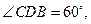
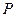 为
为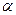 内的动点,且
内的动点,且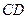 的距离为
的距离为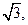 则
则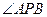 的最大值为________________.
的最大值为________________.