题目内容
(本小题满分12分)
如图(1)是一正方体的表面展开图,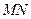 和
和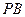 是两条面对角线,请在图(2)的正方体中将
是两条面对角线,请在图(2)的正方体中将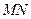 和
和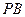 画出来,并就这个正方体解决下面问题.
画出来,并就这个正方体解决下面问题.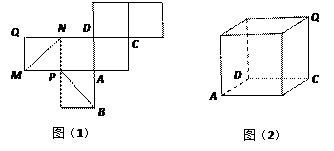
(Ⅰ)求证: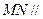 平面
平面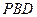 ;
;
(Ⅱ)求证: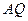 ⊥平面
⊥平面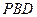 ;
;
(Ⅲ)求二面角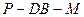 的大小.
的大小.
解:MN、PB的位置如右图示. ……………………………………………………(2分)
(Ⅰ)∵ND//MB且ND=MB,∴四边形NDBM为平行四边形.
∴MN//DB.
∵BD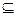 平面PBD,MN
平面PBD,MN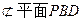 ,∴MN//平面PBD.(5分)
,∴MN//平面PBD.(5分)
(Ⅱ)∵QC⊥平面ABCD,BD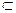 平面ABCD,∴BD⊥QC.
平面ABCD,∴BD⊥QC.
又∵BD⊥AC,∴BD⊥平面AQC.
∵AQ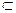 面AQC,∴AQ⊥BD.
面AQC,∴AQ⊥BD.
同理可得AQ⊥PB.
∵BD PD=B,∴AQ⊥面PDB. …………………………(8分)
PD=B,∴AQ⊥面PDB. …………………………(8分)
(Ⅲ)解法1:分别取DB、MN中点E、F,连结PE 、EF、PF.
、EF、PF.
∵在正方体中,PB=PD,∴PE⊥DB.
∵四边形NDBM为矩形,∴EF⊥DB.
∴∠PEF为二面角P—DB—M为平面角.
∵EF⊥平面PMN,∴EF⊥PF.
设正方体的棱长为a,则在直角三角形EFP中,
∵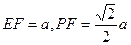 ,∴
,∴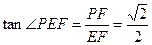 .
.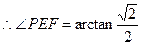 .…………………………(12分)
.…………………………(12分)
解法2:设正方体的棱长为a,以D为坐标原点建立空间直
角坐标系如图.
则点A(a,0,0),P(a,0,a),Q(0,a,a).
∴ .
.
∵PQ⊥面DBM,由(2)知AQ⊥面PDB.
∴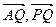 分别为平面PDB、平面DBM的法向量.
分别为平面PDB、平面DBM的法向量.
∴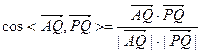
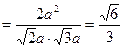 .
.
∴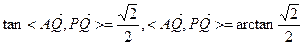 .…………………………(12分)
.…………………………(12分)
解析

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目