题目内容
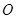 是
是 所在的平面内的一点,且满足
所在的平面内的一点,且满足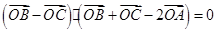 ,则
,则 的形状一定为( )
的形状一定为( )
| A.正三角形 | B.直角三角形 | C.等腰三角形 | D.斜三角形 |
C
解析试题分析:利用向量的加法和减法可得,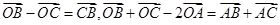 ,根据向量加法的平行四边形法则可得
,根据向量加法的平行四边形法则可得 过BC边的中线,因为
过BC边的中线,因为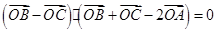 ,所以
,所以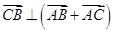 ,即
,即 为BC边的中垂线,故A点在BC的中垂线上,即三角形ABC为等腰三角形,故选C.
为BC边的中垂线,故A点在BC的中垂线上,即三角形ABC为等腰三角形,故选C.
考点:向量加法减法 内积

练习册系列答案
相关题目
在平行四边形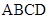 中,
中,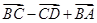 等于 ( )
等于 ( )
A.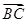 | B.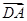 | C.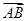 | D.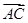 |
已知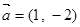 ,
,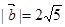 ,且
,且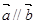 ,则
,则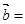 ( )
( )
A.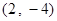 | B.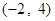 | C.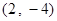 或 或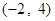 | D.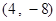 |
在平行四边形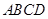 中,
中,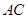 与
与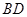 交于点
交于点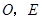 是线段
是线段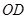 的中点,
的中点,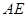 的延长线与
的延长线与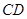 交于点
交于点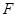 .若
.若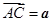 ,
,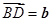 ,则
,则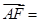 ( )
( )
A.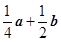 | B.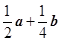 | C. | D. |
已知 和点
和点 满足
满足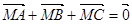 .若存在实数
.若存在实数 使得
使得 成立,则
成立,则 =( )
=( )
| A.2 | B.3 | C.4 | D.5 |
若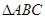 外接圆的半径为1,圆心为O.且
外接圆的半径为1,圆心为O.且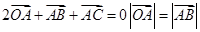 ,则
,则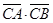 等于( )
等于( )
A.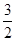 | B.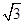 | C.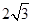 | D.3 |
如图,在 中,
中, ,延长
,延长 到
到 ,使
,使 ,若
,若 ,则
,则 的值是 ( )
的值是 ( )
A. | B. | C. | D. |
设a,b是不共线的两个向量,其夹角是θ,若函数f(x)=(xa+b)·(a-xb)(x∈R)在(0,+∞)上有最大值,则( )
| A.|a|<|b|,且θ是钝角 |
| B.|a|<|b|,且θ是锐角 |
| C.|a|>|b|,且θ是钝角 |
| D.|a|>|b|,且θ是锐角 |
已知向量a与b的夹角为120°,|a|=3,|a+b|=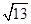 则|b| 等于( ).
则|b| 等于( ).
| A.5 | B.4 | C.3 | D.1 |