题目内容
设函数f(x)=|1-
|(x>0).
(1)作出函数f(x)=|1-
|(x>0)的图象;
(2)当0<a<b,且f(a)=f(b)时,求
+
的值;
(3)若方程f(x)=m有两个不相等的正根,求m的取值范围.
分析:(1)将函数写成分段函数,先作出函数f(x)=1-
(x>0),再将x轴下方部分翻折到x轴上方即可得到函数的图象;
(2)根据函数的图象,可知f(x)在(0,1]上是减函数,而在(1,+∞)上是增函数,利用0<a<b且f(a)=f(b),即可求得
+
的值;
(3)构造函数y
1=f(x),y
2═m,由函数f(x)的图象可得结论.
解答: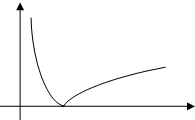
解:(1)函数f(x)=|1-
|=
.
先作出函数f(x)=1-
(x>0),再将x轴下方部分翻折到x轴上方即可得到函数的图象.如图所示
(2)根据函数的图象,可知f(x)在(0,1]上是减函数,而在(1,+∞)上是增函数,
由0<a<b且f(a)=f(b)得0<a<1<b,∴
-1=1-,∴
+
=2
(3)构造函数y
1=f(x),y
2═m,由函数f(x)的图象可知,当0<m<1时,方程f(x)=m有两个不相等的正根.
点评:本题考查绝对值函数,考查数形结合的数学思想,考查学生的作图能力,正确作图是关键.
练习册系列答案
相关题目
 解:(1)函数f(x)=|1-
解:(1)函数f(x)=|1- 解:(1)函数f(x)=|1-
解:(1)函数f(x)=|1-