题目内容
下列各组命题中,满足“‘p或q’为真、‘p且q’为假、‘非p’为真”的是( )
| A、p:0=φ;q:0∈φ | ||||
| B、p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数 | ||||
C、p:a+b≥2
| ||||
D、p:圆(x-1)2+(y-2)2=1的面积被直线x=1平分;q:椭圆
|
分析:先由题设中的关系“‘p或q’为真、‘p且q’为假、‘非p’为真”得出p,q两命题的真假性,再对四个选项中的命题进行判断,得出正确选项
解答:解:由题意“‘p或q’为真、‘p且q’为假、‘非p’为真”可得p是假命题,q是真命题
A选项不符合题意,因为p,q都 是假命题
B选项中p:在△ABC中,若cos2A=cos2B,则A=B是真命题;q:y=sinx在第一象限是增函数是假命题,故不合题意
C选项正确,p:a+b≥2
(a,b∈R)只有在a,b是正数时成立,假命题;q:不等式|x|>x的解集是(-∞,0)是真命题,故C是符合题意的选项;
D选项不正确,由于p:圆(x-1)2+(y-2)2=1的面积被直线x=1平分,是一个真命题;故D选项不合题意
综上知,C是正确选项
故选C
A选项不符合题意,因为p,q都 是假命题
B选项中p:在△ABC中,若cos2A=cos2B,则A=B是真命题;q:y=sinx在第一象限是增函数是假命题,故不合题意
C选项正确,p:a+b≥2
| ab |
D选项不正确,由于p:圆(x-1)2+(y-2)2=1的面积被直线x=1平分,是一个真命题;故D选项不合题意
综上知,C是正确选项
故选C
点评:本题考查复合命题的真假,正确解答本题,关键是理解“‘p或q’为真、‘p且q’为假、‘非p’为真”,由此关系得出两命题的真假来,对四个选项中的命题涉及的知识点的理解与掌握也是解题的关系,基础知识的扎实掌握是解答此类题的知识保证.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各组命题中,满足“p或q”为真、“p且q”为假,“非p”为真的是( )
| A、p:0=∅;q:0∈∅ | ||
| B、p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数 | ||
C、p:a+b≥2
| ||
| D、p:圆(x-1)2+(y-2)2=1的面积被直线x=1平分;q:?x∈{1,-1,0},2x+1>0 |
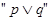 为真,
为真,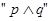 为假,
为假,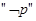 为真的是
为真的是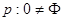 ;
;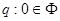
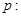 在
在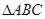 中,若
中,若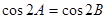 ,则
,则

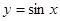 在第一象限是增函数
在第一象限是增函数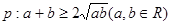
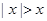 的解集为
的解集为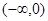
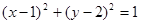 的面积被
的面积被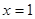 平分
平分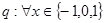 ,
,