题目内容
下列各组命题中,满足“p或q”为真、“p且q”为假,“非p”为真的是( )
| A、p:0=∅;q:0∈∅ | ||
| B、p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数 | ||
C、p:a+b≥2
| ||
| D、p:圆(x-1)2+(y-2)2=1的面积被直线x=1平分;q:?x∈{1,-1,0},2x+1>0 |
分析:由条件“p或q”为真、“p且q”为假,“非p”为真可知p假q真,对照选择项逐一判断.
解答:解:由条件“p或q”为真、“p且q”为假,“非p”为真可知p假q真.
A中,p、q为假命题,不满足题意.
B中,p:在△ABC中,因为0<A,B<π,所以0<2A,2B<2π,故若cos2A=cos2B,则A=B为真,q为假,不满足题意.
C中,p是假命题,因为a,b应该为正实数才对,q为真命题,故C正确.
D中,p是真命题,因为x=1过圆心(1,2),不满足题意.
故选C
A中,p、q为假命题,不满足题意.
B中,p:在△ABC中,因为0<A,B<π,所以0<2A,2B<2π,故若cos2A=cos2B,则A=B为真,q为假,不满足题意.
C中,p是假命题,因为a,b应该为正实数才对,q为真命题,故C正确.
D中,p是真命题,因为x=1过圆心(1,2),不满足题意.
故选C
点评:本题考查复合命题真假的判断,涉及面较广,应细心判断.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各组命题中,满足“‘p或q’为真、‘p且q’为假、‘非p’为真”的是( )
| A、p:0=φ;q:0∈φ | ||||
| B、p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数 | ||||
C、p:a+b≥2
| ||||
D、p:圆(x-1)2+(y-2)2=1的面积被直线x=1平分;q:椭圆
|
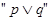 为真,
为真,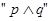 为假,
为假,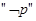 为真的是
为真的是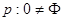 ;
;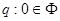
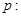 在
在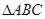 中,若
中,若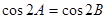 ,则
,则

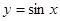 在第一象限是增函数
在第一象限是增函数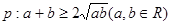
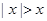 的解集为
的解集为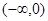
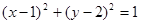 的面积被
的面积被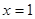 平分
平分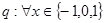 ,
,