题目内容
已知函数

(1)求函数 的单调增区间;
的单调增区间;
(2)若 ,求函数
,求函数 在[1,e]上的最小值.
在[1,e]上的最小值.
(1)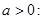
 的单调递增区间为
的单调递增区间为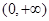 ,
,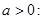
 的单调递增区间为
的单调递增区间为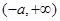 ;
;
(2)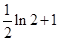 .
.
解析试题分析:(1)可求得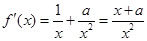 ,结合函数的定义域为
,结合函数的定义域为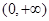 ,需对a的正负形进行分类讨论,从而得到f(x)的单调区间;(2)根据(1)中得到的f(x)的单调性,可得f(x)在
,需对a的正负形进行分类讨论,从而得到f(x)的单调区间;(2)根据(1)中得到的f(x)的单调性,可得f(x)在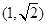 上单调递减,在
上单调递减,在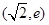 上单调递增,因此f(x)的最小值即为
上单调递增,因此f(x)的最小值即为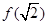 .
.
(1)由题意, 的定义域为
的定义域为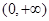 ,且
,且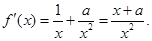 1分
1分
①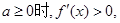
 的单调递增区间为
的单调递增区间为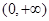 4分
4分
② 当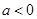 时,令
时,令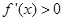 ,得
,得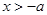 ,∴
,∴ 的单调递增区间为
的单调递增区间为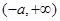 7分
7分
(2)由(1)可知,
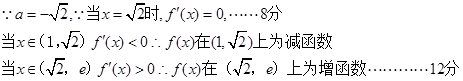
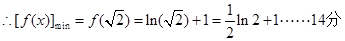 .
.
考点:1、三角恒等变换;2、三角函数的基本运算,3、利用定积分求曲边图形的面积.

练习册系列答案
相关题目
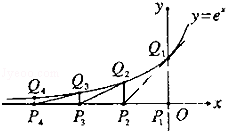
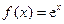 ,其中
,其中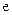 为自然对数的底数.
为自然对数的底数.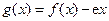 的单调区间;
的单调区间; 在点
在点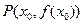 (其中
(其中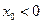 )处的切线为
)处的切线为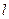 ,
,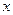 轴、
轴、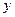 轴所围成的三角形面积为
轴所围成的三角形面积为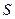 ,求
,求 +alnx(x>0).
+alnx(x>0). [f(x1)+f(x2)]≥f
[f(x1)+f(x2)]≥f 成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.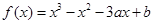 .
.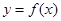 在点
在点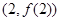 处与直线
处与直线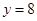 相切,求a,b的值;
相切,求a,b的值; 的单调区间.
的单调区间. 在区间
在区间 上为单调增函数,求
上为单调增函数,求 的取值范围.
的取值范围.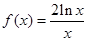
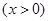
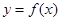 在
在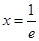 处的切线的斜率;
处的切线的斜率;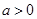 ,求函数
,求函数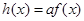 在
在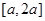 上的最大值.
上的最大值.