题目内容
在关于人体脂肪含量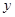 (百分比)和年龄
(百分比)和年龄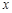 关系的研究中,得到如下一组数据
关系的研究中,得到如下一组数据
|
年龄 |
23 |
27 |
39 |
41 |
45 |
50 |
|
脂肪含量 |
9.5 |
17.8 |
21.2 |
25.9 |
27.5 |
28.2 |
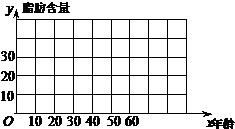
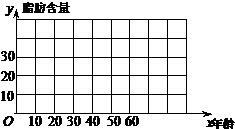
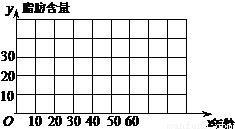
(Ⅰ)画出散点图,判断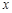 与
与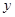 是否具有相关关系;
是否具有相关关系;
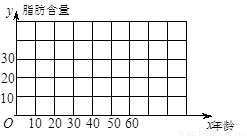
(Ⅱ)通过计算可知 ,
,
请写出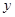 对
对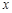 的回归直线方程,并计算出
的回归直线方程,并计算出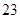 岁和
岁和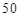 岁的残差.
岁的残差.
【答案】
(Ⅰ)从图中可看出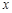 与
与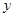 具有相关关系.
具有相关关系.

(Ⅱ)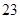 岁和
岁和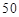 岁的残差分别为
岁的残差分别为 和
和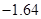 .
.
【解析】
试题分析:(Ⅰ)涉及两个变量,年龄与脂肪含量.
因此选取年龄为自变量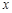 ,脂肪含量为因变量
,脂肪含量为因变量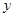 .
.
作散点图,从图中可看出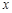 与
与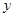 具有相关关系.
具有相关关系.
┄┄┄┄┄┄┄┄┄┄┄┄5分
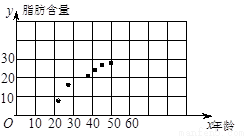
(Ⅱ)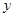 对
对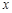 的回归直线方程为
的回归直线方程为
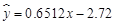 .
.
当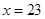 时,
时,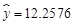 ,
,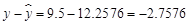 .
.
当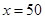 时,
时,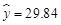 ,
,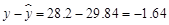 .
.
所以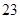 岁和
岁和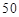 岁的残差分别为
岁的残差分别为 和
和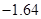 .
10分
.
10分
考点:本题主要考查散点图,相关性,线性回归直线方程,残差的概念。
点评:中档题,正相关,两个变量变动方向相同,一个变量由大到小或由小到大变化时,另一个变量亦由大到小或由小到大变化。负相关,两个变量变动方向相同,一个变量由大到小或由小到大变化时,另一个变量亦由小到大或由大到小变化。从散点图看,就是自左向右升(降)。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


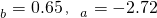 ,请写出y对x的回归直线方程,并计算出23岁和50岁的残差.
,请写出y对x的回归直线方程,并计算出23岁和50岁的残差.
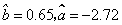 ,请写出y对x的回归直线方程,并计算出23岁和50岁的残差。
,请写出y对x的回归直线方程,并计算出23岁和50岁的残差。 
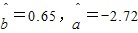 ,请写出y对x的回归直线方程,并计算出23岁和50岁的残差.
,请写出y对x的回归直线方程,并计算出23岁和50岁的残差.