题目内容
在关于人体脂肪含量y(百分比)和年龄x关系的研究中,得到如下一组数据

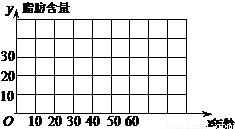
(Ⅰ)画出散点图,判断x与y是否具有相关关系;
(Ⅱ)通过计算可知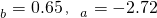 ,请写出y对x的回归直线方程,并计算出23岁和50岁的残差.
,请写出y对x的回归直线方程,并计算出23岁和50岁的残差.
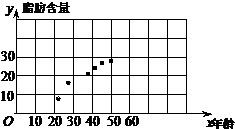 解:(Ⅰ)涉及两个变量:年龄与脂肪含量.
解:(Ⅰ)涉及两个变量:年龄与脂肪含量.∴选取年龄为自变量x,脂肪含量为因变量y.
作散点图,从图中可看出x与y具有相关关系.
(Ⅱ)y对x的回归直线方程为
 =0.65x-2.72.
=0.65x-2.72.当x=23时,
 =12.23,y-
=12.23,y- =9.5-12.23=-2.73
=9.5-12.23=-2.73当x=50时,
 =29.78,y-
=29.78,y- =28.2-29.78=-1.58.
=28.2-29.78=-1.58.∴23岁和50岁的残差分别为-2.73和-1.58.
分析:(I)本题涉及两个变量年龄与脂肪含量.可以选取年龄为自变量x,脂肪含量为因变量y.在坐标系中描点作出散点图,从图中可看出x与y具有相关关系.
(II)根据所给的线性回归方程的系数,写出线性回归方程,代入自变量的值做出y的预报值,同数据组所给的Y的值做差,得到23岁和50岁的残差.
点评:本题考查可线性化的回归分析,考查求自变量的预报值,考查求自变量对应的残差,是一个综合题目,有点省份已经作为高考题目出现过.

练习册系列答案
相关题目

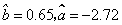 ,请写出y对x的回归直线方程,并计算出23岁和50岁的残差。
,请写出y对x的回归直线方程,并计算出23岁和50岁的残差。 
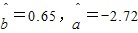 ,请写出y对x的回归直线方程,并计算出23岁和50岁的残差.
,请写出y对x的回归直线方程,并计算出23岁和50岁的残差.
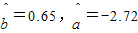 ,请写出y对x的回归直线方程,并计算出23岁和50岁的残差.
,请写出y对x的回归直线方程,并计算出23岁和50岁的残差.