题目内容
已知函数
且f（4）
（1）求m的值;
（2）判定f（x）的奇偶性;
（3）判断f（x）在（0,+∞）上的单调性,并给予证明．
解:（1）因为f（4）=
,所以4m-
=,所以m=1．
（2）因为f（x）的定义域为{x|x≠0},又
（x）,所以f（x）是奇函数．
（3）设x1>x2>0,则
因为x1>x2>0,所以x1-x2>0,1+
>0,所以f（x1）>f（x2）,所以f（x）在（0,+∞）上为单调递增函数．
（或用求导数的方法）
练习册系列答案
相关题目
且f(4)
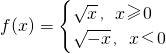且f（a）+f（4）=4，那么a=-4；
且f（4）=0．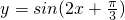
的图象，只要将y=sin2x的图象向左平移
单位；