题目内容
17.已知集合A=|x|x>1|,B=|xy=$\sqrt{9-{x}^{2}}$|.那么A∩B=( )| A. | [-3,3] | B. | (-1,3] | C. | (1,3] | D. | (1,3) |
分析 先化简B={x|-3≤x≤3},再根据交集运算的定义即得结果.
解答 解:根据题意可知$B=\{x|\sqrt{9-{x}^{2}}≥0\}$={x|-3≤x≤3},
由于A={x|x>1},
所以A∩B={x|1<x≤3},
故选:C.
点评 本题考查集合的交集运算,先化简集合B是解题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知圆x2+y2=5上两点A、B与坐标原点O恰构成正三角形,则向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的数量积是( )
| A. | $\frac{5}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{5\sqrt{5}}{2}$ |
8.若复数z=$\frac{2}{1-i}$,则( )
| A. | 1-i | B. | -1-i | C. | 1+i | D. | -1+i |
9.某赛事组委会要为获奖者定做某工艺品作为奖品,其中一等奖奖品3件,二等奖奖品6件.制作一等奖和二等奖奖品所用原料完全相同,但工艺不同,故价格有所差异.现有甲、乙两家工厂可以制作奖品(一等奖、二等奖奖品均符合要求),甲厂收费便宜,但原料有限,最多只能制作4件奖品,乙厂原料充足,但收费较贵,其具体收费情况如下表:
则组委会定做该工艺品的费用总和最低为4900元.
奖品 收费(元/件) 工厂 | 一等奖奖品 | 二等奖奖品 |
| 甲 | 500 | 400 |
| 乙 | 800 | 600 |
 的图象不过原点,且关于原点对称,则
的图象不过原点,且关于原点对称,则 的取值是( )
的取值是( )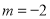 B.
B.
 或
或 D.
D.