题目内容
（本小题满分12分）
某货轮在A处看灯塔B在货轮北偏东
，距离为
n mile；在A处看灯塔C在货轮的北偏西
，距离为
n mile.货轮由A处向正北航行到D处时，再看灯塔B在北偏东
，求：
（Ⅰ）A处与D处之间的距离；
（Ⅱ）灯塔C与D处之间的距离.
某货轮在A处看灯塔B在货轮北偏东
，距离为n mile；在A处看灯塔C在货轮的北偏西，距离为n mile.货轮由A处向正北航行到D处时，再看灯塔B在北偏东，求：（Ⅰ）A处与D处之间的距离；
（Ⅱ）灯塔C与D处之间的距离.
（Ⅰ）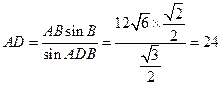
（Ⅱ）灯塔C与D处之间的距离为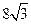
n mile.
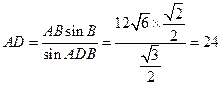
（Ⅱ）灯塔C与D处之间的距离为
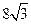n mile.解：（Ⅰ
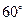）在△ABD中，由已知得 ∠ADB=
，B=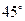
．
由正弦定理得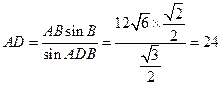．…………6分
（Ⅱ）在△ADC中，由余弦定理得
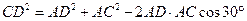，解得CD= 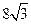.所以A处与D处之间的距离为24 n mile，灯塔C与D处之间的距离为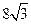n mile. …………12分
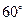）在△ABD中，由已知得 ∠ADB=，B=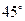．由正弦定理得
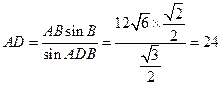．…………6分（Ⅱ）在△ADC中，由余弦定理得
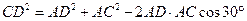，解得CD= 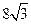.所以A处与D处之间的距离为24 n mile，灯塔C与D处之间的距离为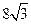n mile. …………12分
练习册系列答案
相关题目
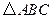中，
，
． 
的值； （Ⅱ）设
，求
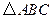中，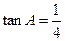
，
.
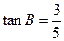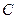的大小； （Ⅱ）若
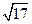，求最小边的边长．
（其中0≤t≤20）给出，F（t）的单位是辆／分，t的单位是分，则在下列哪个时间段内车流量是增加的 （ ）
、
、
分别是角A、B、Ｃ、的对边，如果
成等差数列，且
，
，那么
B. 
C. 
D.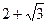 
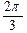，轮船A的航行速度为25 千米/小时，轮船B的航行速度是15 千米/小时，下午2时两艘船的距离是多少？
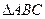中，
，则此三角形解的情况有（ ）
一解 
两解 
一解或两解 
无解