题目内容
某公路段在某一时刻内监测到的车速频率分布直方图如图所示.
(Ⅰ)求纵坐标中参数h的值及第三个小长方形的面积;
(Ⅱ)求车速的众数v1,中位数v2的估计值;
(Ⅲ)求平均车速 的估计值.
的估计值.
(Ⅰ)0.4;(Ⅱ)62.5;(Ⅲ)62.
解析试题分析:(Ⅰ)所有小长形面积之和为1,由此求出h=0.01,从而能求出第三个小长方形的面积.(Ⅱ)利用频率分布直方图估计车速的众数就是最高矩形方框中点的横坐标,而车速的中位数就是在中位数两边直方图的面积相等.(Ⅲ)利用频率分布直方图及估值公式: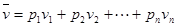 (其中
(其中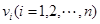 是各直方图的中点的横坐标,
是各直方图的中点的横坐标,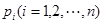 是各直方图的面积)能求出平均车速
是各直方图的面积)能求出平均车速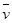 .
.
试题解析:(Ⅰ)∵所有小长形面积之和为1,
∴10h+10×3h+10×4h+10×2h=1,
解得h=0.01,
∴第三个小长方形的面积为:10×4h=10×0.04=0.4.
(Ⅱ)车速的众数v1=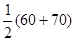 =65,
=65,
车速的中位数是两边直方图的面积相等,
于是得:10×0.01+10×0.03+(v2﹣60)×0.04=0.5,
解得v2=62.5.
(Ⅲ)平均车速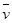 =0.01×10×45+0.03×10×55+0.04×10×65+0.02×10×75=62.
=0.01×10×45+0.03×10×55+0.04×10×65+0.02×10×75=62.
考点:频率分布直方图的应用.

某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为: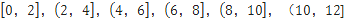 .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.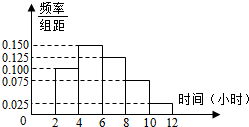
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有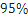 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附:K2=
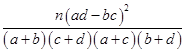
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(1)用分层抽样的方法在喜欢打蓝球的学生中抽6人,其中男生抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女生的概率.
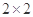 列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系?
列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系?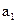 ,
, ,
, 的方差是2,则样本2
的方差是2,则样本2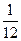 ,则总体中的个体数为 。
,则总体中的个体数为 。