Question

如图在直三棱柱ABC-A₁B₁C₁中，棱AB，BC，BB₁两两垂直且长度相等，点P在线段A₁C₁上运动，异面直线BP与B₁C所成的角为θ，则θ的取值范围是（　　）

• A．

  π

  3

  ≤θ≤

  π

  2

• B．0＜θ≤

  π

  2

• C．

  π

  3

  ≤θ＜

  π

  2

• D．0＜θ≤

  π

  3

Answer 1

分析：建立空间直角坐标系，设棱长为1，设P（-a，1-a，1）（0＜a≤1），则

BP

=（-a，1-a，1），

B1C

=（0，1，-1），利用向量的夹角公式，即可求得结论．

解答：解：建立如图所示的空间直角坐标系，设棱长为1，

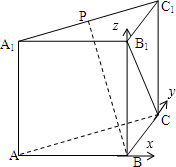
则B（0，0，0），C（0，1，0），B₁（0，0，1）
设P（-a，1-a，1）（0＜a≤1），则

BP

=（-a，1-a，1），

B1C

=（0，1，-1）
∴cosθ=|

BP • B1C

| BP || B1C |

|=|

-a

2a2-2a+2 × 2

|=

1

2

×

1

a+ 1 a -1

≤

1

2

∵0＜θ＜

π

2

∴

π

3

≤θ＜

π

2

∴θ的取值范围是[

π

3

，

π

2

)．
故选C．

点评：本题考查线线角，考查利用向量知识解决空间角问题，属于中档题．