Question

【题目】已知函数h（x）=ax3﹣1（a∈R），g（x）=lnx，f（x）=h（x）+3xg（x）（e为自然对数的底数）．
（I）若f（x）图象过点（1，﹣1），求f（x）的单调区间；
（II）若f（x）在区间（ ，e）上有且只有一个极值点，求实数a的取值范围；
（III）函数F（x）=（a﹣ ）x3+ x2g（a）﹣h（x）﹣1，当a＞e 时，函数F（x）过点A（1，m）的切线至少有2条，求实数m的值．

Answer 1

【答案】解：（Ⅰ）由已知f（x）=h（x）+3xg（x）=ax3﹣1+3xlnx，
又f（x）过点（1，﹣1），所以a=0，
∴f（x）=3xlnx﹣1，且定义域为（0，+∞），
f′（x）=3lnx+3=3（lnx+1），
令f′（x）＞0，解得：x＞ ，令f′（x）＜0，解得：0＜x＜ ，
故f（x）=3xlnx﹣1在（0， ）上是减函数，在（ ，+∞）上是增函数；
（Ⅱ）函数f（x）=ax3+3xlnx﹣1的定义域为（0，+∞），
f′（x）=3（ax2+lnx+1），
令r（x）=ax2+lnx+1，
则r′（x）=2ax+ = ，
当a＞0时，r′（x）＞0在（0，+∞）恒成立，
故f′（x）=3（ax2+lnx+1）在（0，+∞）上是增函数，
而f′（ ）= ＞0，
故当x∈（ ，e）时，f′（x）＞0恒成立，
故f（x）在区间（ ，e）上单调递增，
故f（x）在区间（ ，e）上没有极值点；
当a=0时，由（Ⅰ）知，f（x）在区间（ ，e）上没有极值点；
当a＜0时，令 =0，解得，x= ；
故r（x）=ax2+lnx+1在（0， ）上是增函数，在（ ，+∞）上是减函数，
①当r（e）r（ ）＜0，即﹣ ＜a＜0时，
r（x）在（ ，e）上有且只有一个零点，且在该零点两侧异号，
②令r（ ）=0，得 =0，不成立；
③令r（e）=0，得a=﹣ ，所以 ∈（ ，e），
而r（ ）=r（ ）= +ln ＞0，又r（ ）＜0，
所以r（x）在（ ，e）上有且只有一个零点，且在该零点两侧异号，
综上所述，实数a的取值范围是[﹣ ，0）．
（Ⅲ）函数F（x）=（a﹣ ）x3+ x2g（a）﹣h（x）﹣1，
由函数F（x）过点A（1，m）的切线，
所以m= x03﹣（1+ lna）x02+x0lna，（*）
②据题意，原命题等价于关于x0的方程（*）至少有2个不同的解．
设φ（x）= x3﹣（1+ lna）x2+xlna，
φ′（x）=2x2﹣（2+lna）x+lna=（x﹣1）（2x﹣lna），
因为a＞ ，所以 lna＞ ＞1，
当x∈（﹣∞，1）和（ lna，+∞）时，φ′（x）＞0，φ（x）为增函数；
当x∈（1， lna）时，φ′（x）＜0，φ（x）为减函数；
所以φ（x）的极大值为φ（1）= lna﹣ ，
φ（x）的极小值为φ（ lna）=﹣ ln3a+ ln2a，
设lna=t，t＞ ，
则原命题等价于 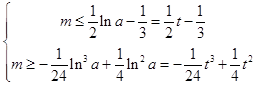对t＞ 恒成立，
所以由m≤ t﹣ 对t＞ 恒成立，得m≤ ； （1）
记s（t）=﹣ t3+ t2 ， s′（t）=﹣ t2+ t= t（1﹣ t），
所以t＞ 时，s（t）的最大值为s（4）= ，由m≥﹣ t3+ t2对t＞ 恒成立，得m≥ ． （2）
由（1）（2）得，m= ．
综上，当a＞ ，实数m的值为 时，函数F（x）过点A（1，m）的切线至少有2条
【解析】（Ⅰ）求出f（x）的导数，解关于导函数的不等式，求出函数的单调区间即可；（Ⅱ）求出f（x）的导数，通过讨论a的范围求出函数的单调区间，结合已知条件求出a的范围即可；（Ⅲ）求出函数的导数，求出B处的切线方程，根据函数的单调性求出a的范围即可．
【考点精析】认真审题，首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减)，还要掌握函数的极值与导数(求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值)的相关知识才是答题的关键．