Question

（本小题满分12分）如图，AB为圆O的直

径，点E、F在圆O上，AB∥EF，矩形ABCD

所在的平面和圆O所在的平面垂直，且.

⑴求证：；

⑵设FC的中点为M，求证：；

⑶设平面CBF将几何体分成的两个锥体的体积分别为，求的值.

 

Answer 1

【答案】

 

（1）略

（2）略

（3）

【解析】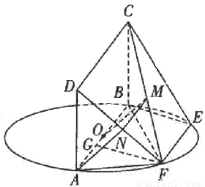证明：⑴由平面ABCD⊥平面ABEF，CD⊥AB，平面ABCD∩平面ABEF=AB，

得CD⊥平面ABEF，而AF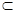平面ABEF，所以 AF⊥CB，

又因AB为圆O的直径，所以 AF⊥BF，BFC∩B=B，所以 AF⊥平面CBF．　　　　　　　　　　　……４分

⑵ 设DF的中点为N，连接AN和MN，则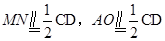，所以 ，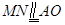

  四边形MNAO为一平行四边形，又AN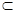平面DAF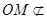，平面DAF，

  所以.　　　　　　　　　　　　　　　　　　　　　　　　　……８分

⑶ 过点F作FG⊥AB于G，因为平面ABCD⊥平面ABEF，

所以FG⊥平面ABCD，所以.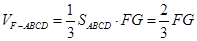

因为CB⊥平面ABEF，所以

 .

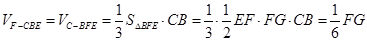所以 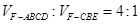……１２分