题目内容
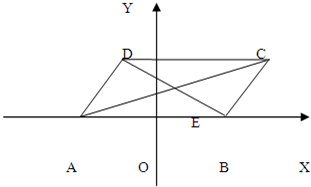 已知□ABCD,A(-2,0),B(2,0),且|AD|=2
已知□ABCD,A(-2,0),B(2,0),且|AD|=2(1)求□ABCD对角线交点E的轨迹方程.
(2)过A作直线交以A、B为焦点的椭圆于M、N两点,且|MN|=
| 8 |
| 3 |
| 2 |
| 4 |
| 3 |
(3)与E点轨迹相切的直线l交椭圆于P、Q两点,求|PQ|的最大值及此时l的方程.
分析:(1)设E(x,y),D(x0,y0),根据ABCD是平行四边形,可得
+
=2
,从而可得坐标之间的关系,再利用|AD|=2,我们就可以求得平行四边形ABCD对角线交点E的轨迹方程;
(2)先根据A、B为焦点的椭圆的焦距2c=4,则c=2,设椭圆方程为
+
=1,即
+
=1,将y=k(x+2)代入,再利用韦达定理及MN中点到y轴的距离为
,|MN|=
,可得k2=
,进而我们就可以求出所求椭圆方程;
(3)由(1)可知点E的轨迹是圆x2+y2=1设(x0,y0)是圆上的任一点,则过(x0,y0)点的切线方程是x0x+y0y=1,再分y0≠0,y0=0去求切线长名酒可以得出结论.
| AB |
| AD |
| AE |
(2)先根据A、B为焦点的椭圆的焦距2c=4,则c=2,设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| a2-4 |
| 4 |
| 3 |
| 8 |
| 3 |
| 2 |
| 9a2-64 |
| 8 |
(3)由(1)可知点E的轨迹是圆x2+y2=1设(x0,y0)是圆上的任一点,则过(x0,y0)点的切线方程是x0x+y0y=1,再分y0≠0,y0=0去求切线长名酒可以得出结论.
解答:解:(1)设E(x,y),D(x0,y0)
∵ABCD是平行四边形,∴
+
=2
,
∴(4,0)+(x0+2,y0)=2(x+2,y)
∴(x0+6,y0)=(2x+4,2y)
∴
⇒
又|AD|=2,∴(x0+2)2+y02=4,
∴(2x-2+2)2+(2y)2=4
即:x2+y2=1
∴平行四边形ABCD对角线交点E的轨迹方程为x2+y2=1
(2)设过A的直线方程为y=k(x+2)
以A、B为焦点的椭圆的焦距2c=4,则c=2
设椭圆方程为
+
=1,即
+
=1…(*)
将y=k(x+2)代入(*)得
+
=1
即 (a2+a2k2-4)x2+4a2k2x+4a2k2-a4+4a2=0
设M(x1,y1),N(x2,y2)
则x1+x2=
,x1•x2=
∵MN中点到Y轴的距离为
,且MN过点A,而点A在y轴的左侧,
∴MN中点也在y轴的左侧.
∴
=
,
∴a2k2=2a2-8,
∴x1+x2=
,x1•x2=
∴(x1-x2)2=(x1+x2)2-4x1x2=(
)2-
(8-a2)
∵|MN|=
∴
|x1-x2|=
∴(1+k2)(
-
+
a2)=
即 12a2+12a2k2-32k2=160
∴12a2+12(2a2-8)-32k2=160
∴k2=
∴a2•
=2a2-8,
∴9a4-80a2+64=0
∴(a2-8)(9a2-8)=0,
∵a>c=2,
∴a2=8
∴b2=a2-c2=8-4=4
∴所求椭圆方程为
+
=1
(3)由(1)可知点E的轨迹是圆x2+y2=1
设(x0,y0)是圆上的任一点,则过(x0,y0)点的切线方程是x0x+y0y=1
①当y0≠0时,y=
代入椭圆方程得:
(2x02+y02)x2-4x0x+2-32y02=0,
又x02+y02=1
∴(x02+1)x2-4x0x+32x02-30=0x1+x2=
,x1x2=
∴(x1-x2)2=(x1+x2)2-4x1x2=
(-128x04+8x02+120)|PQ|2=(1+(-
)2)(x1-x2)2=
(x1-x2)2
=
•
(-128x04+8x02+120)=
令16x02+15=t(15≤t<31)
则|PQ|2=
=
=
,
∵15≤t<31
∴当t=15时,|PQ|2取最大值为15,|PQ|的最大值为
.
此时 16x02=0,x0=0,∴y0=1,
∴直线l的方程为y=±1
②当y0=0时,求得|PQ|=
<
故:所求|PQ|的最大值为
,此时l的方程为y=±1
∵ABCD是平行四边形,∴
| AB |
| AD |
| AE |
∴(4,0)+(x0+2,y0)=2(x+2,y)
∴(x0+6,y0)=(2x+4,2y)
∴
|
|
又|AD|=2,∴(x0+2)2+y02=4,
∴(2x-2+2)2+(2y)2=4
即:x2+y2=1
∴平行四边形ABCD对角线交点E的轨迹方程为x2+y2=1
(2)设过A的直线方程为y=k(x+2)
以A、B为焦点的椭圆的焦距2c=4,则c=2
设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| a2-4 |
将y=k(x+2)代入(*)得
| x2 |
| a 2 |
| k2(x+2)2 |
| a2-4 |
即 (a2+a2k2-4)x2+4a2k2x+4a2k2-a4+4a2=0
设M(x1,y1),N(x2,y2)
则x1+x2=
| 4a2k2 |
| 4-a2-a2k2 |
| 4a2k2-a4+4a2 |
| a2+a2k2-4 |
∵MN中点到Y轴的距离为
| 4 |
| 3 |
∴MN中点也在y轴的左侧.
∴
| 2a2k2 |
| a2+a2k2-4 |
| 4 |
| 3 |
∴a2k2=2a2-8,
∴x1+x2=
| -8 |
| 3 |
| 8-a2 |
| 3 |
∴(x1-x2)2=(x1+x2)2-4x1x2=(
| 8 |
| 3 |
| 4 |
| 3 |
∵|MN|=
| 8 |
| 3 |
| 2 |
∴
| 1+k2 |
| 8 |
| 3 |
| 2 |
∴(1+k2)(
| 64 |
| 9 |
| 32 |
| 3 |
| 4 |
| 3 |
| 128 |
| 9 |
即 12a2+12a2k2-32k2=160
∴12a2+12(2a2-8)-32k2=160
∴k2=
| 9a2-64 |
| 8 |
∴a2•
| 9a2-64 |
| 8 |
∴9a4-80a2+64=0
∴(a2-8)(9a2-8)=0,
∵a>c=2,
∴a2=8
∴b2=a2-c2=8-4=4
∴所求椭圆方程为
| x2 |
| 8 |
| y2 |
| 4 |
(3)由(1)可知点E的轨迹是圆x2+y2=1
设(x0,y0)是圆上的任一点,则过(x0,y0)点的切线方程是x0x+y0y=1
①当y0≠0时,y=
| 1-x0x |
| y0 |
(2x02+y02)x2-4x0x+2-32y02=0,
又x02+y02=1
∴(x02+1)x2-4x0x+32x02-30=0x1+x2=
| 4x0 |
| x02+1 |
| 32x02-30 |
| x02+1 |
∴(x1-x2)2=(x1+x2)2-4x1x2=
| 1 |
| (x02+1)2 |
| x0 |
| y0 |
| x02+y02 |
| y02 |
=
| 1 |
| 1-x02 |
| 1 |
| (1+x02)2 |
| 16x02+15 |
| (1+x02)2 |
令16x02+15=t(15≤t<31)
则|PQ|2=
| t | ||
(
|
| 256t |
| t2+2t+1 |
| 256 | ||
t+
|
∵15≤t<31
∴当t=15时,|PQ|2取最大值为15,|PQ|的最大值为
| 15 |
此时 16x02=0,x0=0,∴y0=1,
∴直线l的方程为y=±1
②当y0=0时,求得|PQ|=
| 7 |
| 15 |
故:所求|PQ|的最大值为
| 15 |
点评:直线与圆锥曲线的综合,通常都是直线代入圆锥曲线,利用韦达定理进行解决,求解圆锥曲线方程问题,待定系数法是常用方法.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
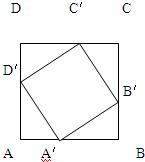 已知ABCD,A'B'C'D'都是正方形(如图),而A'、B'、C'、D'分别把AB、BC、CD、DA分为m:n,设AB=1.
已知ABCD,A'B'C'D'都是正方形(如图),而A'、B'、C'、D'分别把AB、BC、CD、DA分为m:n,设AB=1.
 .
.